證明與圓的切線在切點處的垂線經過圓心。

待辦事項

我們需要證明與圓的切線在切點處的垂線經過圓心。

解答

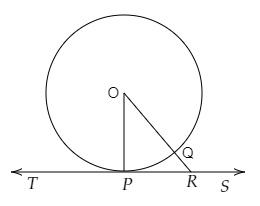
設 $TS$ 是以 $O$ 為圓心，在 $P$ 點與圓相切的切線。

連線 $OP$。

畫一條直線 $OR$，該直線與圓相交於 $Q$ 點，並與切線 $TS$ 相交於 $R$ 點。

$OP = OQ$ (圓的半徑)

$OQ

$\Rightarrow OP

同樣地，

$OP$ 小於從 $O$ 到 $TS$ 的所有其他直線。

$OP$ 是最短的直線。

因此，

$OP$ 垂直於 $TS$。

透過 $P$ 的垂線將經過圓心。

證畢。 

教程點

更新於： 2022年10月10日

54 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

立即開始