證明連線圓的兩條平行切線的切點的線段經過圓心。

已知：圓的兩條平行切線和連線這兩條切線的切點的線段。

要求：證明該線段經過圓心。

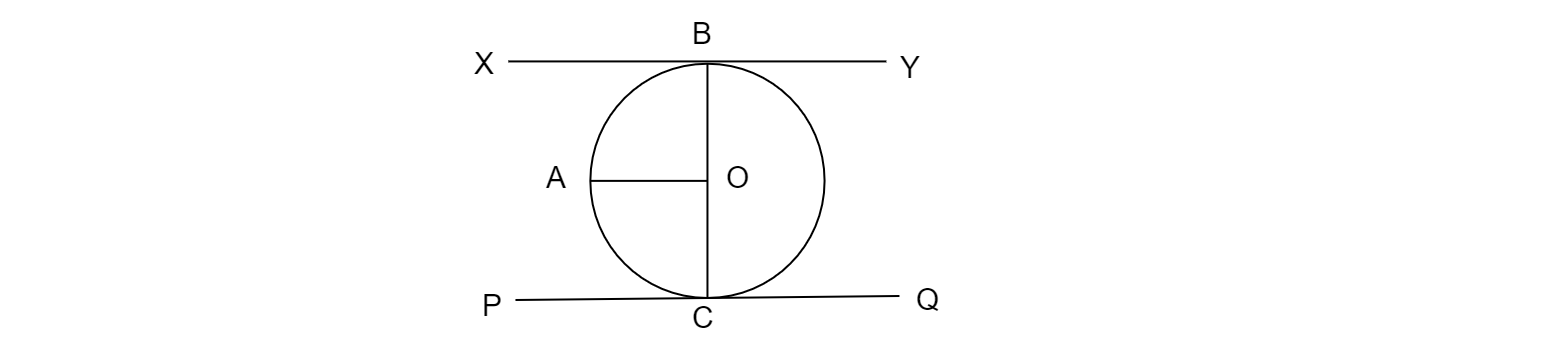
設 XBY 和 PCQ 是圓的兩條平行切線，圓心為 O。

連線 OB 和 OC。

現在，$XB\parallel AO$

我們知道鄰補角的和為 $180^{o}$。

$\therefore \ \angle XBO+\angle AOB=180^{o}$

$\angle XBO=90^{o} \ (圓的切線垂直於過切點的半徑)$

$\Rightarrow 90^{o} +\angle AOB=180^{o}$

$\Rightarrow \angle AOB=90^{o}$

類似地，$\angle AOC=90^{o} $

$\angle BOC=\angle AOB+\angle AOC=90^{o}+90^{o}=180^{o}$

因此，我們發現 $\angle BOC$ 是一條過圓心 O 的直線。

或者我們可以說 BC 是一條過圓心 O 的直線。

因此，證明了連線圓的切線的切點 B 和 C 的線段經過圓心。