證明兩條平行切線之間的切線截距在圓心處構成直角。

待辦事項

我們必須證明兩條平行切線之間的切線截距在圓心處構成直角。

解答

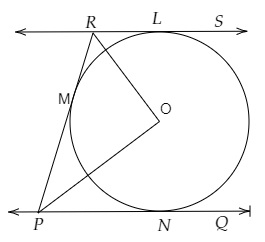
設PQ和RS是圓的兩條平行切線。

RMP是PQ和RS之間切線的截距。
連線RO和PQ，其中O是圓心。

RL和RM是切線，連線RO。

這意味著：

∠LRO = ∠MRO .......(i)

同樣地：

PM和PN是切線，連線PO。

∠NPO = ∠MPO .......(ii)

將方程式(i)和(ii)相加，我們得到：

∠LRO + ∠NPO = ∠MRO + ∠MPO

∠LRM + ∠MPN = 180° (同旁內角)

⇒ ∠LRO + ∠MRO + ∠MPO + ∠NPO = 180°

⇒ ∠MRO + ∠MRO + ∠MPO + ∠MPO = 180°

⇒ 2(∠MRO + ∠MPO) = 180°

⇒ ∠MRO + ∠MPO = 180°/2 = 90°

在△POR中：

∠MRO + ∠MPO + ∠POR = 180°

⇒ 90° + ∠POR = 180°

⇒ ∠POR = 180° - 90°

∠POR = 90°

證畢。

教程點

更新於：2022年10月10日

85 次瀏覽

啟動您的職業生涯

完成課程獲得認證

開始