證明：平分圓內弦的直徑也平分該弦在圓心處所張的角。

待辦事項

我們需要證明：平分圓內弦的直徑也平分該弦在圓心處所張的角。

解答

設在圓心為O的圓中，CD為直徑，AB為弦

且直徑在E點平分弦AB。

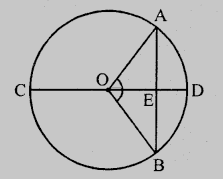
連線OA和OB。

在△OAE和△OBE中，

OA = OB             (圓的半徑)

OE = OE           (公共邊)

AE = EB          (已知)

因此，根據SSS公理，

△OAE ≅ △OBE

這意味著，

∠AOE = ∠BOE         (全等三角形對應角相等)

因此，直徑平分弦所張的角。

證畢。

教程點

更新於：2022年10月10日

253 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習