證明圓的直徑兩端所作的切線平行。

待辦事項

我們需要證明圓的直徑兩端所作的切線平行。

解答

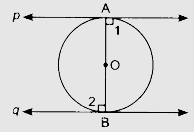
設 $AB$ 為圓的直徑，$p$ 和 $q$ 為兩條切線。

$OA \perp p$

$OB \perp q$

$\angle 1 = \angle 2 = 90^o$

這意味著，

$p \| q$          (垂直於同一條直線的兩條直線互相平行)

證畢。

教程點

更新於: 2022年10月10日

343 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習