資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律蘇尚特有一個倒置圓錐形容器，頂部開口，高11釐米，頂部半徑為2.5釐米，容器中裝滿了水。他將一些直徑為0.5釐米的金屬球體放入容器中，導致容器中$\frac{2}{5}$的水流出。求放入容器中的球體數量。蘇尚特將流出的水用於灌溉花壇。蘇尚特體現了怎樣的價值觀？
已知：圓錐形容器的高$=11\ cm$。容器頂部的半徑$=2.5\ cm$。金屬球體的直徑=0.5 cm。從容器中流出的水量$=$容器中水的$\frac{2}{5}$。
要求：求放入容器中的球體數量。
解答
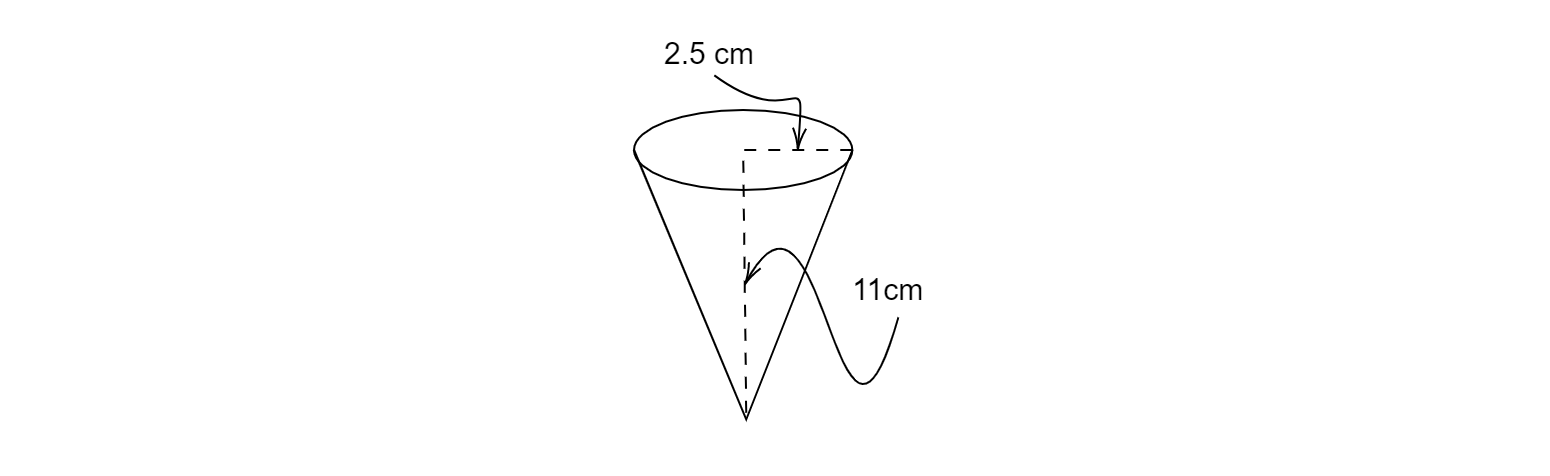
圓錐形容器的高 (h) $= 11\ cm$
圓錐形容器的半徑$( r_{1})$ $=2.5\ cm$
金屬球體的半徑$( r_{2})$ $=\frac{0.5}{2}= 0.25\ cm$
設放入容器中的球體數量為n
流失的水體積$=$放入容器中的球體體積
$\frac{2}{5}\times$ 圓錐體積$=n\times$ 一個球體的體積
$\Rightarrow \frac{2}{5}\times\frac{1}{3}\pi r^{2}_{1}h=n\times\frac{4}{3}\pi r^{3}_{2}$
$\Rightarrow r^{2}_{1}h=n\times10r^{3}_{2}$
$\Rightarrow ( 2.5)^2\times11=n\times10\times( 0.25)^{3}$
$\Rightarrow 68.75=0.15625n$
$\Rightarrow n=\frac{68.75}{0.15625}$
$\Rightarrow n=440$
因此，放入容器中的球體數量為440個。
蘇尚特將流出的水用於灌溉花壇。這體現了合理利用水的價值觀。
更新時間： 2022年10月10日
瀏覽量：284
廣告