求由直線 $x+y=10$ 和兩個座標軸圍成的面積。

已知：直線 $x+y=10$。

求解：求由直線 $x+y=10$ 和兩個座標軸圍成的面積。

已知 $x+y=10$

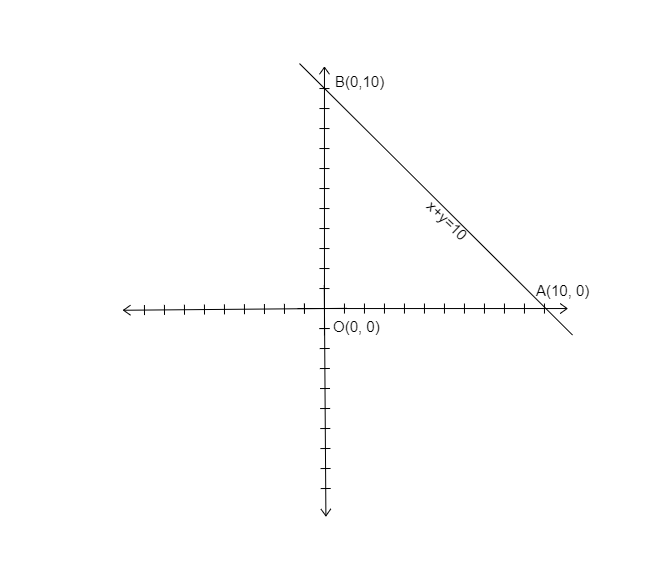
如果 $x=0\ \ \Rightarrow y=10$

如果 $x=10\ \ \Rightarrow y=0$

$\therefore$ 這三個點是 $O( 0,\ 0),\ A( 10,\ 0)$ 和 $B( 0,\ 10)$

使用面積公式

面積$=\frac{1}{2}[x_1( y_2-y_3)+x_2( y_3-y_1)+x_3( y_1-y_2)]$

$=\frac{1}{2}[0( 0-10)+10( 10-0)+0( 0−0)]$

$=\frac{1}{2}\times100=50\ 平方單位$。