生成式AI模型中機率密度函式的作用

---

---

機率分佈可以是離散的或連續的。

• 離散機率分佈更適合於結果只能取離散或分類隨機變數的場景。
• 當結果在連續的值範圍內取任何值時，連續機率分佈更合適。

在生成建模的背景下，連續機率分佈作為一種強大的工具，旨在在廣泛的應用中建立逼真且多樣化的資料樣本。事實上，它們幫助生成模型更好地理解和模擬現實世界的資料。

連續機率分佈背後的關鍵概念之一是機率密度函式（PDF），它描述了連續隨機變數（如時間、重量或高度）在給定範圍內取特定值的可能性。在本章中，我們將詳細地解釋機率密度函式。

理解機率密度函式（PDF）

對於離散變數，我們可以很容易地計算機率。但是，另一方面，對於連續變數，計算機率相當困難，因為機率取一系列無限的值。在統計學中，描述此類變數機率的函式稱為機率密度函式（PDF）。

簡單來說，機率密度函式是一個定義連續隨機變數（例如X）與其機率之間關係的函式。我們可以使用該函式找到變數X的機率。

在數學上，連續隨機變數X的PDF f(x)必須滿足以下屬性：

• $\mathrm{f(x) \geq 0}$ 對於X範圍內的所有x。
• PDF曲線在X所有可能取值上的總面積等於1。這表示總機率空間。
• X落在特定區間[a,b]內的機率由f(x)在該區間上的積分給出：$\mathrm{\int_{a}^{b} \: f(x) \: dx}$。

繪製PDF後，我們將得到如下圖形：

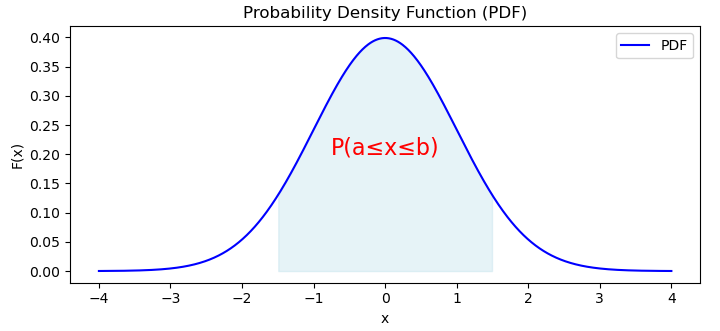
機率分佈函式是機率論中的一個基本概念，它為我們提供了機率分佈的連續表示，使我們能夠理解在連續域中不同結果發生的可能性。它廣泛應用於機器學習、統計學和物理學等各個領域。

使用Python實現機率密度函式

在Python中，要找到給定資料集的機率密度函式（PDF），我們可以使用NumPy和Matplotlib等庫。下面是一個計算和繪製資料集PDF的簡單示例：

示例

# importing necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Creating Sample dataset 
data = np.random.normal(loc=0, scale=1, size=1000)

# Fit a Gaussian distribution to the data
mu, std = norm.fit(data)

# Plot the histogram of the data
plt.figure(figsize=(7.2, 2.5))
plt.hist(data, bins=50, density=True, alpha=0.5, color='cyan')

# Plot the PDF of the fitted Gaussian distribution
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, mu, std)
plt.plot(x, p, 'g', linewidth=2)

plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.title('Probability Density Function (PDF)')
plt.grid(True)

plt.show()

在上面的程式碼中，我們首先使用NumPy的np.random.normal()函式生成一個隨機資料集。

然後，我們使用SciPy的norm.fit()將高斯分佈擬合到資料。此函式返回擬合的高斯分佈的均值（mu）和標準差（std）。

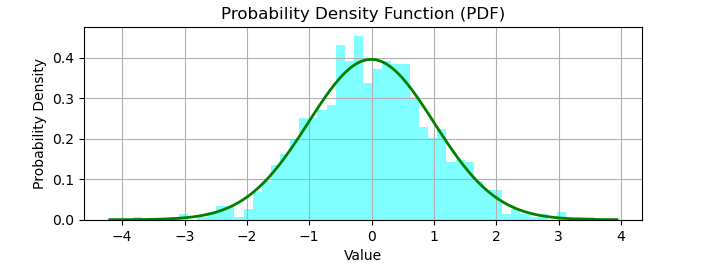
之後，我們使用Matplotlib的plt.hist()繪製資料的直方圖。最後，我們在直方圖上繪製平滑的鐘形曲線（PDF）。

輸出

執行此程式碼後，您將獲得如下輸出圖形：

機率密度函式在生成建模中的作用

在生成建模中，機率密度函式（PDF）發揮著幾個關鍵作用，如下所示：

建模資料分佈

建模資料分佈是生成建模中的重要任務之一。眾所周知，機率密度函式提供了潛在資料分佈的數學表示。PDF幫助生成模型最佳地描述觀察到的資料。

資料取樣

一旦生成模型學習了PDF，它就可以用於從建模的資料分佈中取樣新的資料點。此取樣過程幫助生成模型生成與原始資料非常相似的新資料樣本。

似然估計

許多生成建模演算法（如最大似然估計（MLE）和變分推斷）都使用似然估計。PDF透過估計給定分佈引數下觀察到特定資料點的可能性來幫助生成模型。

生成對抗網路（GAN）

在GAN中，我們有一個稱為生成器的網路。生成器透過捕獲潛在資料分佈來學習生成逼真的資料樣本。它通常輸出遵循連續分佈的資料點，並且與此分佈相關的機率密度函式指導學習過程。

變分自動編碼器（VAE）

VAE學習一個低維潛在空間，該空間捕獲資料的顯著特徵。機率密度函式用於對潛在變數的分佈進行建模。它允許模型透過從該潛在空間中取樣並將樣本解碼到原始資料空間來生成新的資料樣本。

模型效能評估

機率密度函式也可用於評估生成模型的效能。一些指標（如對數似然或散度度量）量化了學習到的分佈與真實資料分佈的匹配程度。它為我們提供了對生成樣本質量的見解。

結論

在本章中，我們詳細解釋了機率密度函式（PDF）、其在Python中的實現及其在生成建模中的多方面作用。

PDF是機率論中的一個基本概念，它為我們提供了機率分佈的連續表示，幫助我們理解在連續域中不同結果發生的可能性。我們瞭解了PDF如何定義連續隨機變數與其機率之間的關係。

我們還透過一個示例演示瞭如何使用Python實現機率密度函式。機率密度函式是生成建模中必不可少的工具，它能夠表示、取樣和評估資料分佈，並作為各種生成建模演算法的基礎。