生成式AI模型 - 最大似然估計

---

---

最大似然估計 (MLE) 是一種統計方法，它提供了一種主要方法來估計機率分佈的引數，該分佈最能描述給定的資料集。MLE 假設指定的分佈生成了資料。簡單來說，MLE 是一種用於找出模型未知引數（例如一組資料點的平均值或分佈）最可能值的方法。這就像我們猜測序列中缺失的數字，以便它符合我們已經知道的數字模式。

在生成式 AI 領域，尤其是在生成對抗網路 (GAN) 和變分自編碼器 (VAE) 等生成模型中，MLE 具有廣泛的應用。例如，在生成手寫數字 (0-9) 的影像時，我們希望我們的模型生成的影像類似於我們資料集中（如 MNIST）的影像。我們可以透過最大化給定模型引數的情況下觀察訓練資料的可能性來實現這一點。

maximize Σ log P(x | θ)

我們稍後將在使用 Python 程式語言建立我們的第一個 GAN 模型時詳細介紹這一點。閱讀本章以瞭解最大似然估計的概念、其在生成建模中的重要作用、MLE 在生成建模中的應用及其 Python 實現。

理解最大似然估計 (MLE)

最大似然估計 (MLE) 是一種強大的統計方法，用於根據觀察到的資料估計機率分佈的引數。讓我們藉助其數學基礎更詳細地瞭解它：

MLE 的數學基礎

MLE 的核心是似然函式：$\mathrm{L(\theta | x)}$。這裡，$\mathrm{\theta}$ 表示分佈的引數，x 表示觀察到的資料。

似然函式量化了給定特定引數值的情況下觀察資料的機率。從數學上講，它表示為觀察資料的聯合機率密度函式 (PDF) 或機率質量函式 (PMF)。

$$\mathrm{L(\theta | x) \: = \: f(x | \theta)}$$

為了簡化計算，我們通常使用對數似然函式 $\mathrm{l(\theta | x)}$，它是似然函式的自然對數：

$$\mathrm{l(\theta | x) \: = \: \log L(\theta | x)}$$

實際上，MLE 的目標是找到最大化似然函式 $\mathrm{L(\theta | x)}$ 或等效地最大化對數似然函式 $\mathrm{l(\theta | x)}$ 的引數值 $\mathrm{\hat{\theta}}$：

$$\mathrm{\hat{\theta} \: = \: argmax_{\theta} L(\theta | x)}$$

或者，

$$\mathrm{\hat{\theta} \: = \: argmax_{\theta} l(\theta | x)}$$

現在，為了獲得最大似然估計 $\mathrm{\hat{\theta}}$，我們對對數似然函式 $\mathrm{l(\theta | x)}$ 關於引數 $\mathrm{\theta}$ 求導，並將導數設定為零：

$$\mathrm{\frac{\partial \: l(\theta | x)}{\partial \: \theta} \: = \: 0}$$

求解上述方程得到 MLE $\mathrm{\hat{\theta}}$。

生成建模中的 MLE

正如我們前面討論的，生成建模涉及捕獲資料的潛在分佈並生成與原始訓練資料相當的新資料。在訓練生成模型時，MLE 透過估計潛在機率分佈的引數發揮著至關重要的作用。

讓我們看看如何在生成建模中應用 MLE：

模型選擇

我們首先需要選擇一個能夠捕獲潛在資料分佈的機率模型。一些常見的模型包括高斯分佈、混合模型、神經網路等。

似然函式

接下來，我們需要定義似然函式。此似然函式衡量觀察到給定資料的機率。例如，對於給定的資料集 $\mathrm{D \: = \: \lbrace x_{1},x_{2},x_{3},\: \dots \: x_{n} \rbrace}$，似然函式 $\mathrm{L(\theta | D)}$ 取決於模型引數 $\mathrm{\theta}$，並且由觀察每個資料點的機率的乘積給出：

$$\mathrm{L(\theta | D) \: = \: \prod_{i=1}^N p(x_{i} | \theta)}$$

最大化

現在我們需要根據模型引數 $\mathrm{\theta}$ 最大化似然函式。最大化包括找到使在模型下觀察到的資料最有可能的 $\mathrm{\theta}$ 值。

引數估計

最後，當似然函式最大化時，所得引數值將用作生成模型引數的估計值。這些估計的引數定義了學習到的分佈，然後可以使用它來生成與觀察到的資料相當的新資料點。

MLE 在生成建模中的應用

MLE 在生成建模的各個領域都有廣泛的應用。下面是一些重要的應用：

• 高斯混合模型 (GMM) - MLE 用於估計 GMM 中高斯分量的引數。這些引數能夠對具有多個模式的複雜資料分佈進行建模。
• 變分自編碼器 (VAE) - 在 VAE 中，MLE 用於學習潛在變數分佈的引數。它允許模型透過從此學習到的分佈中取樣來生成新的資料樣本。
• 生成對抗網路 (GAN) - GAN 不直接最佳化似然函式，但 MLE 用於 GAN 的訓練以指導學習過程並提高樣本質量。

使用 Python 實現最大似然估計

我們可以使用 Python 實現 MLE，並使用 Matplotlib 等庫對其進行視覺化。下面是一個簡單的示例，用於執行 MLE 以根據給定的資料集估計高斯分佈的引數：

示例

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# Sample dataset (you can replace this with your own data)
data = np.random.normal(loc=2, scale=1, size=2000)

# Maximum Likelihood Estimation for a Gaussian distribution
def maximum_likelihood_estimation(data):
   # Calculate the mean and standard deviation of the data
   mu = np.mean(data)
   sigma = np.std(data)
   return mu, sigma

# Perform Maximum Likelihood Estimation
estimated_mu, estimated_sigma = maximum_likelihood_estimation(data)

# Generate x values for plotting
x = np.linspace(min(data), max(data), 1000)

# Plot histogram of the data
plt.figure(figsize=(7.2, 5.5))
plt.hist(data, bins=30, density=True, alpha=0.6, color='blue', label='Data Histogram')

# Plot the true Gaussian distribution
plt.plot(x, norm.pdf(x, loc=2, scale=1), color='red', linestyle='--', label='True Gaussian Distribution')

# Plot the estimated Gaussian distribution using MLE
plt.plot(x, norm.pdf(x, loc=estimated_mu, scale=estimated_sigma), color='green', linestyle='-', label='Estimated Gaussian Distribution (MLE)')

plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.title('Maximum Likelihood Estimation for Gaussian Distribution')
plt.legend()
plt.grid(True)

plt.show()

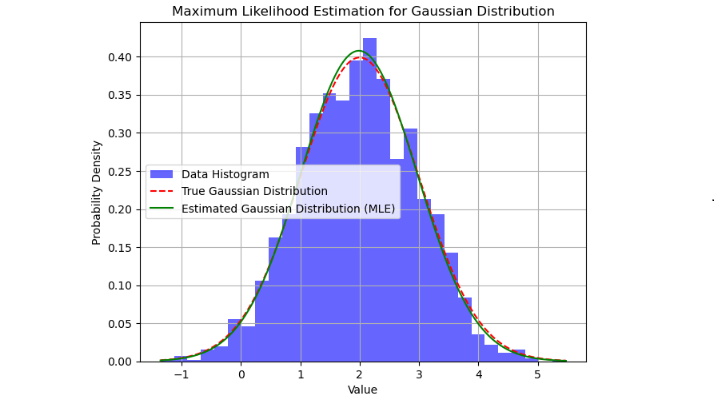
輸出

上面的程式碼將生成一個圖，顯示資料的直方圖、真實的高斯分佈以及使用最大似然估計 (MLE) 獲得的估計高斯分佈。

結論

在本章中，我們強調了 MLE 在生成建模中的重要性。在生成建模中，MLE 作為學習資料分佈和生成新樣本的支柱。

模型選擇、似然函式、最大化和引數估計是我們可以在生成建模中應用 MLE 的步驟。