資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究連續時間系統的級聯形式實現
連續時間系統的實現
連續時間LTI系統的實現意味著獲得與系統微分方程或傳遞函式相對應的網路。
系統的傳遞函式可以透過使用積分器或微分器來實現。由於某些缺點，微分器不用於實現實際系統。因此，僅使用積分器來實現連續時間系統。加法器和乘法器是另外兩個用於實現連續時間系統的元件。
CT系統的級聯形式實現
在連續時間系統的級聯形式實現中，系統的傳遞函式表示為若干一階和二階傳遞函式的乘積，然後使用積分器和加法器實現每個傳遞函式，最後將所有實現的結構級聯，即串聯連線。
第一個結構的輸出連線到第二個結構的輸入，第二個結構的輸出連線到第三個結構的輸入，依此類推。因此，在連續時間系統的級聯形式實現中，輸入連線到第一個結構，輸出從最後一個結構獲取。
以下示例說明了級聯形式中連續時間系統的實現。
數值示例
使用級聯形式實現，實現由傳遞函式描述的連續時間系統。
$$\mathrm{\mathit{H\left ( s \right )\mathrm{\,=\,}\frac{\mathrm{3}\left ( s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{3}s\mathrm{\,+\,}\mathrm{2} \right )}{s^{\mathrm{3}}\mathrm{\,+\,}\mathrm{12}s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{47}s\mathrm{\,+\,}\mathrm{60}}}}$$
解答
給定的傳遞函式為：
$$\mathrm{\mathit{H\left ( s \right )\mathrm{\,=\,}\frac{\mathrm{3}\left ( s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{3}s\mathrm{\,+\,}\mathrm{2} \right )}{s^{\mathrm{3}}\mathrm{\,+\,}\mathrm{12}s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{47}s\mathrm{\,+\,}\mathrm{60}}}}$$
將給定的傳遞函式表示為幾個傳遞函式的乘積，如下所示：
$$\mathrm{\mathit{H\left ( s \right )\mathrm{\,=\,}\frac{\mathrm{3}\left ( s\mathrm{\,+\,}\mathrm{2} \right )\left ( s\mathrm{\,+\,}\mathrm{1} \right )}{\left ( s\mathrm{\,+\,}\mathrm{3} \right )\left ( s\mathrm{\,+\,}\mathrm{4} \right )\left ( s\mathrm{\,+\,}\mathrm{5} \right )}}}$$
$$\mathrm{\mathit{\Rightarrow H\left ( s \right )\mathrm{\,=\,}\left ( \frac{\mathrm{3}}{s\mathrm{\,+\,}\mathrm{3}} \right )\left ( \frac{s\mathrm{\,+\,}\mathrm{2}}{s\mathrm{\,+\,}\mathrm{4}} \right )\left ( \frac{s\mathrm{\,+\,}\mathrm{1}}{s\mathrm{\,+\,}\mathrm{5}} \right )}}$$
令：
$$\mathrm{\mathit{H_{\mathrm{1}}\left ( s \right )\mathrm{\,=\,}\left ( \frac{\mathrm{3}}{s\mathrm{\,+\,}\mathrm{3}} \right )\mathrm{\,=\,}\frac{\mathrm{3}s^{-\mathrm{1}}}{\mathrm{1\mathrm{\,+\,}3}s^{\mathrm{-1}}}}} $$
$$\mathrm{\mathit{H_{\mathrm{2}}\left ( s \right )\mathrm{\,=\,}\left ( \frac{s\mathrm{\,+\,}\mathrm{2}}{s\mathrm{\,+\,}\mathrm{4}} \right )\mathrm{\,=\,}\frac{\mathrm{1\mathrm{\,+\,}2}s^{\mathrm{-1}}}{\mathrm{1\mathrm{\,+\,}4}s^{-\mathrm{1}}}}}$$
$$\mathrm{\mathit{H_{\mathrm{3}}\left ( s \right )\mathrm{\,=\,}\left ( \frac{s\mathrm{\,+\,}\mathrm{1}}{s\mathrm{\,+\,}\mathrm{5}} \right )\mathrm{\,=\,}\frac{\mathrm{1\mathrm{\,+\,}}s^{\mathrm{-1}}}{\mathrm{1\mathrm{\,+\,}5}s^{-\mathrm{1}}}}}$$
每個傳遞函式都可以如下實現：
步驟 1
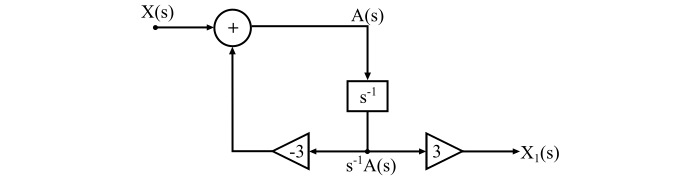
實現 $\mathrm{\mathit{H_{\mathrm{1}}\left ( s \right )}}$ −
$$\mathrm{\mathit{H_{\mathrm{1}}\left ( s \right )\mathrm{\,=\,}\frac{X_{\mathrm{1}}\left ( s \right )}{X\left ( s \right )}\mathrm{\,=\,}\frac{X_{\mathrm{1}}\left ( s \right )}{A\left ( s \right )}\frac{A\left ( s \right )}{X\left ( s \right )}\mathrm{\,=\,}\frac{\mathrm{3}s^{-\mathrm{1}}}{\mathrm{1\mathrm{\,+\,}3}s^{\mathrm{-1}}}}}$$
$$\mathrm{\mathit{\frac{X_{\mathrm{1}}\left ( s \right )}{A\left ( s \right )}\mathrm{\,=\,}\mathrm{3}s^{-\mathrm{1}}}}$$
$$\mathrm{\mathit{\Rightarrow X_{\mathrm{1}}\left ( s \right )\mathrm{\,=\,}\mathrm{3}s^{-\mathrm{1}}A\left ( s \right )}}$$
以及
$$\mathrm{\mathit{\frac{A\left ( s \right )}{X\left ( s \right )}\mathrm{\,=\,}\left ( \frac{\mathrm{1}}{\mathrm{1\mathrm{\,+\,}3}s^{-\mathrm{1}}} \right )}}$$
$$\mathrm{\mathit{\Rightarrow A\left ( s \right )\frac{}{}\mathrm{\,=\,}X\left ( s \right )-\mathrm{3}s^{-\mathrm{1}}A\left ( s \right )}}$$
步驟 2
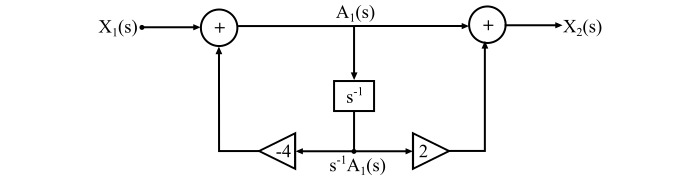
實現 $\mathrm{\mathit{H_{\mathrm{2}}\left ( s \right )}}$ −
$$\mathrm{\mathit{H_{\mathrm{2}}\left ( s \right )\mathrm{\,=\,}\frac{X_{\mathrm{2}}\left ( s \right )}{X_{\mathrm{1}}\left ( s \right )}\mathrm{\,=\,}\frac{X_{\mathrm{2}}\left ( s \right )}{A_{\mathrm{1}}\left ( s \right )}\frac{A_{\mathrm{1}}\left ( s \right )}{X_{\mathrm{1}}\left ( s \right )}\mathrm{\,=\,}\frac{\mathrm{1\mathrm{\,+\,}2}s^{\mathrm{-1}}}{\mathrm{1\mathrm{\,+\,}4}s^{-\mathrm{1}}}}}$$
$$\mathrm{\mathit{\Rightarrow \frac{X_{\mathrm{2}}\left ( s \right )}{A_{\mathrm{1}}\left ( s \right )}\mathrm{\,=\,}\mathrm{1}\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}}}$$
$$\mathrm{\mathit{\Rightarrow X_{\mathrm{2}}\left ( s \right )\mathrm{\,=\,}A_{\mathrm{1}}\left ( s \right )\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}A\left ( s \right )}}$$
以及，
$$\mathrm{\mathit{\frac{A_{\mathrm{1}}\left ( s \right )}{X_{\mathrm{1}}\left ( s \right )}\mathrm{\,=\,}\frac{\mathrm{1}}{\mathrm{1\mathrm{\,+\,}4}s^{\mathrm{-1}}}}}$$
$$\mathrm{\mathit{\Rightarrow A_{\mathrm{1}}\left ( s \right )\mathrm{\,=\,}X_{\mathrm{1}}\left ( s \right )-\mathrm{4}s^{\mathrm{-1}}A_{\mathrm{1}}\left ( s \right )}}$$
步驟 3
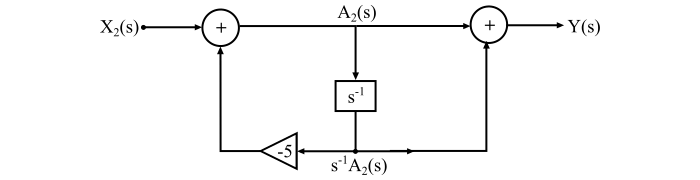
實現 $\mathrm{\mathit{H_{\mathrm{3}}\left ( s \right )}}$ −
$$\mathrm{\mathit{H_{\mathrm{3}}\left ( s \right )\mathrm{\,=\,}\frac{Y\left ( s \right )}{X_{\mathrm{2}}\left ( s \right )}\mathrm{\,=\,}\frac{Y\left ( s \right )}{A_{\mathrm{2}}\left ( s \right )}\frac{A_{\mathrm{2}}\left ( s \right )}{X_{\mathrm{2}}\left ( s \right )}\mathrm{\,=\,}\frac{\mathrm{1\mathrm{\,+\,}}s^{\mathrm{-1}}}{\mathrm{1\mathrm{\,+\,}5}s^{-\mathrm{1}}}}}$$
$$\mathrm{\mathit{\Rightarrow \frac{Y\left ( s \right )}{A_{\mathrm{2}}\left ( s \right )}\mathrm{\,=\,}\mathrm{1\mathrm{\,+\,}}s^{\mathrm{-1}}}}$$
$$\mathrm{\mathit{\Rightarrow Y\left ( s \right ) \mathrm{\,=\,}A_{\mathrm{2}}\left ( s \right )\mathrm{\,+\,}s^{\mathrm{-1}}A_{\mathrm{2}}\left ( s \right )}}$$
以及，
$$\mathrm{\mathit{\frac{A_{\mathrm{2}}\left ( s \right )}{X_{\mathrm{2}}\left ( s \right )}\mathrm{\,=\,}\frac{\mathrm{1}}{\mathrm{1\mathrm{\,+\,}5}s^{\mathrm{-1}}}}}$$
$$\mathrm{\mathit{\Rightarrow A_{\mathrm{2}}\left ( s \right )\mathrm{\,=\,}X_{\mathrm{2}}\left ( s \right )-\mathrm{5}s^{\mathrm{-1}}A_{\mathrm{2}\left ( s \right )}}}$$
步驟 4
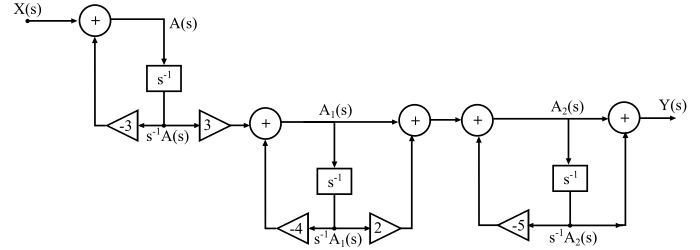
現在，將上述三個結構級聯連線以獲得系統傳遞函式 H(s) 的級聯實現，如下圖所示。
5K+ 閱讀量
