連續時間系統的直接型 I 實現
連續時間系統的實現
連續時間 LTI 系統的實現意味著獲得對應於系統微分方程或傳遞函式的網路。
系統的傳遞函式可以透過使用積分器或微分器來實現。由於某些缺點,微分器不用於實現實際系統。因此,僅使用積分器來實現連續時間系統。加法器和乘法器是另外兩個用於實現連續時間系統的元件。
CT 系統的直接型 I 實現
直接型 I 實現是實現連續時間系統最簡單、最直接的結構。在連續時間系統的直接型 I 實現中,描述系統的微分方程或傳遞函式是使用輸入和輸出變數的單獨積分器直接實現的。因此,要使用直接型 I 實現系統,需要更多數量的積分器。因此,它更復雜。
直接型 I 實現提供了時域和 s 域方程之間的直接關係。對於連續時間系統的直接型實現,輸出變數用方程中所有其他項表示。
數值示例
使用直接型 I 實現,實現由以下傳遞函式描述的系統:
$$\mathrm{\mathit{H\left ( s \right )\mathrm{\,=\,}\frac{Y\left ( s \right )}{X\left ( s \right )}\mathrm{\,=\,}\frac{s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{4}s\mathrm{\,+\,}\mathrm{3}}{s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{2}s\mathrm{\,+\,}\mathrm{5}}}}$$
解答
為了實現由傳遞函式 H(s) 描述的系統,首先將 H(s) 的分子和分母表示為 𝑠−1 的冪,如下所示:
$$\mathrm{\mathit{H\left ( s \right )\mathrm{\,=\,}\frac{Y\left ( s \right )}{X\left ( s \right )}\mathrm{\,=\,}\frac{s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{4}s\mathrm{\,+\,}\mathrm{3}}{s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{2}s\mathrm{\,+\,}\mathrm{5}}\mathrm{\,=\,}\frac{\mathrm{1}\mathrm{\,+\,}\mathrm{4}s^{\mathrm{-1}}\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}}}{\mathrm{1}\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}\mathrm{\,+\,}\mathrm{5}s^{\mathrm{-2}}} }}$$
交叉相乘,我們得到:
$$\mathrm{\mathit{Y\left ( s \right )\left [ \mathrm{1}\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}\mathrm{\,+\,}\mathrm{5}s^{\mathrm{-2}} \right ]\mathrm{\,=\,}X\left ( s \right )\left [ \mathrm{1}\mathrm{\,+\,}\mathrm{4}s^{\mathrm{-1}}\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}} \right ]}}$$
$$\mathrm{\mathit{\Rightarrow Y\left ( s \right )\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}Y\left ( s \right )\mathrm{\,+\,}\mathrm{5}s^{\mathrm{-2}}Y\left ( s \right )\mathrm{\,=\,}X\left ( s \right )\mathrm{\,+\,}\mathrm{4}s^{\mathrm{-1}}X\left ( s \right )\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}}X\left ( s \right )}}$$
$$\mathrm{\mathit{\Rightarrow Y\left ( s \right )\mathrm{\,=\,}X\left ( s \right )\mathrm{\,+\,}\mathrm{4}s^{\mathrm{-1}}X\left ( s \right )\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}}X\left ( s \right )-\mathrm{2}s^{\mathrm{-1}}Y\left ( s \right )-\mathrm{5}s^{\mathrm{-2}}Y\left ( s \right )}}$$
令:
$$\mathrm{\mathit{X\left ( s \right )\mathrm{\,+\,}\mathrm{4}s^{\mathrm{-1}}X\left ( s \right )\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}}X\left ( s \right )\mathrm{\,=\,}A\left ( s \right)}}$$
$$\mathrm{\mathit{\therefore Y\left ( s \right )\mathrm{\,=\,}A\left ( s \right )-\mathrm{2}s^{\mathrm{-1}}Y\left ( s \right )-\mathrm{5}s^{\mathrm{-2}}Y\left ( s \right )}}$$
該方程可以如下實現:
步驟 1
實現 A(s) 如下所示:
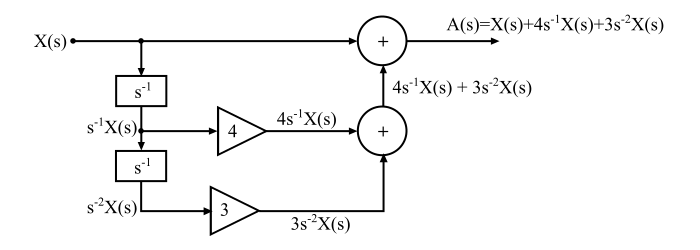
步驟 2
根據 A(s) 實現 Y(s) 如下所示:
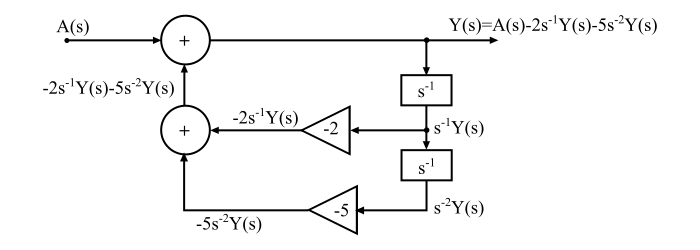
步驟 3
將以上兩個結果結合起來,得到直接型 I 實現如下所示:
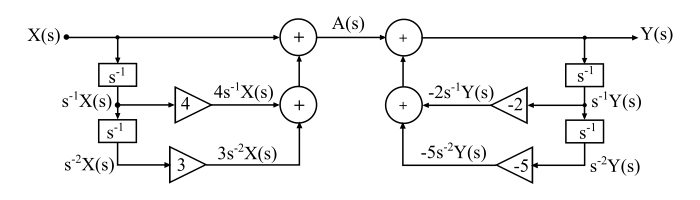


 資料結構
資料結構 網路
網路 關係資料庫管理系統 (RDBMS)
關係資料庫管理系統 (RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 語言程式設計
C 語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP