連續時間系統的直接Ⅱ型實現
連續時間系統的實現
連續時間LTI系統的實現是指獲得與系統微分方程或傳遞函式對應的網路。
系統的傳遞函式可以透過使用積分器或微分器來實現。由於某些缺點,微分器不用於實現實際系統。因此,僅使用積分器來實現連續時間系統。加法器和乘法器是用於實現連續時間系統的另外兩個元件。
連續時間系統的直接Ⅱ型實現
連續時間系統的直接Ⅱ型實現的優點是它使用最少的積分器數量。在這種實現結構中,中間變數被積分,而不是分別使用單獨的積分器來積分輸入和輸出變數。
以下示例說明了連續時間系統的直接Ⅱ型實現:
數值示例
使用直接Ⅱ型實現,實現由以下傳遞函式描述的連續時間LTI系統。
$$\mathrm{\mathit{H\left ( s \right )\mathrm{\,=\,}\frac{Y\left ( s \right )}{X\left ( s \right )}\mathrm{\,=\,}\frac{s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{2}s\mathrm{\,+\,}\mathrm{3}}{s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{2}s\mathrm{\,+\,}\mathrm{5}}}}$$
解答
給定函式需表示為s的負冪:
$$\mathrm{\mathit{H\left ( s \right )\mathrm{\,=\,}\frac{Y\left ( s \right )}{X\left ( s \right )}\mathrm{\,=\,}\frac{s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{2}s\mathrm{\,+\,}\mathrm{3}}{s^{\mathrm{2}}\mathrm{\,+\,}\mathrm{2}s\mathrm{\,+\,}\mathrm{5}}\mathrm{\,=\,}\frac{\mathrm{1}\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}}}{\mathrm{1}\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}\mathrm{\,+\,}\mathrm{5}s^{\mathrm{-2}}} }}$$
令A(s) = 1,則將給定的傳遞函式分解為兩部分:
$$\mathrm{\mathit{H\left ( s \right )\mathrm{\,=\,}\frac{Y\left ( s \right )}{X\left ( s \right )}\mathrm{\,=\,}\frac{Y\left ( s \right )}{A\left ( s \right )}\frac{A\left ( s \right )}{X\left ( s \right )}}}$$
其中,
$$\mathrm{\mathit{\frac{Y\left ( s \right )}{A\left ( s \right )}\mathrm{\,=\,}\mathrm{1}\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}}\; \; \; \cdot \cdot \cdot \left ( \mathrm{1} \right )}}$$
以及
$$\mathrm{\mathit{\frac{A\left ( s \right )}{X\left ( s \right )}\mathrm{\,=\,}\frac{\mathrm{1}}{\mathrm{1}\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}\mathrm{\,+\,}\mathrm{5}s^{\mathrm{-2}}}\; \; \; \cdot \cdot \cdot \left ( \mathrm{2} \right )}}$$
將式(1)和式(2)交叉相乘,我們得到:
從式(1),
$$\mathrm{\mathit{Y\left ( s \right )\mathrm{\,=\,}A\left ( s \right )\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}A\left ( s \right )\mathrm{\,+\,}\mathrm{3}s^{\mathrm{-2}}A\left ( s \right )}}$$
從式(2),
$$\mathrm{\mathit{X\left ( s \right )\mathrm{\,=\,}A\left ( s \right )\mathrm{\,+\,}\mathrm{2}s^{\mathrm{-1}}A\left ( s \right )\mathrm{\,+\,}\mathrm{5}s^{\mathrm{-2}}A\left ( s \right )}}$$
$$\mathrm{\mathit{\Rightarrow A\left ( s \right )\mathrm{\,=\,}X\left ( s \right )-\mathrm{2}s^{\mathrm{-1}}A\left ( s \right )-\mathrm{5}s^{\mathrm{-2}}A\left ( s \right )}}$$
因此,上述傳遞函式可以如下實現:
步驟1
實現A(s)如下:
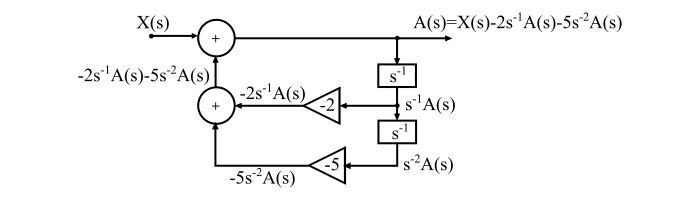
步驟2
實現Y(s)如下:
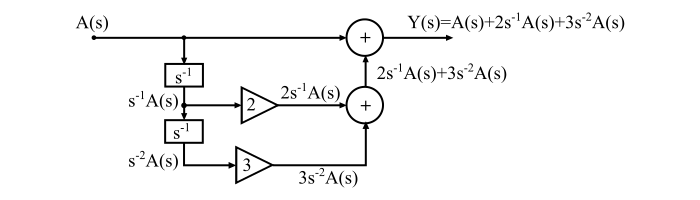
步驟3
透過組合上述兩種實現,我們得到傳遞函式H(s)的直接Ⅱ型實現如下:
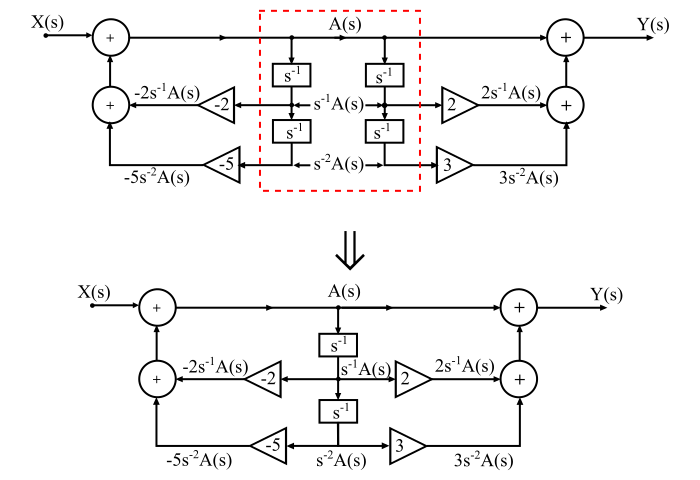


 資料結構
資料結構 網路
網路 關係資料庫管理系統 (RDBMS)
關係資料庫管理系統 (RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C語言程式設計
C語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP