資料結構
網路
關係型資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學訊號與系統——什麼是偶對稱性？
波形對稱性的重要性
如果週期訊號𝑥(𝑡)具有一定的對稱性，則一些三角傅立葉級數係數可能變為零，從而簡化係數的計算。
偶對稱或映象對稱
當週期函式關於垂直軸對稱時，則稱其具有**偶對稱性**或**映象對稱性**。偶對稱性也稱為反射對稱性。數學上，如果週期函式x(t)滿足：
$$\mathrm{𝑥(𝑡) = 𝑥(−𝑡)\:\:\:\:\:\: ...(1)}$$
圖中顯示了一些具有偶對稱性的函式示例。偶函式總是關於垂直軸對稱的。
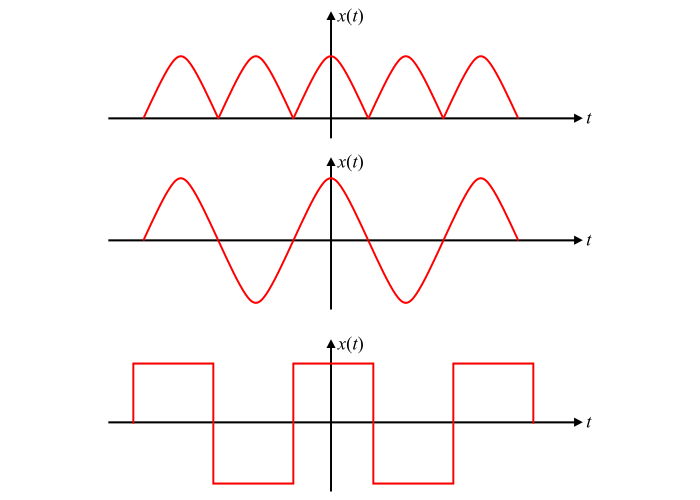
解釋
我們知道，任何週期訊號𝑥(𝑡)都可以分解成偶分量和奇分量，即：
$$\mathrm{𝑥(𝑡) = 𝑥_{𝑒}(𝑡) + 𝑥_{𝑜}(𝑡) … (2)}$$
如果函式𝑥(𝑡)是偶函式，則：
$$\mathrm{𝑥_{𝑜}(𝑡) = 0}$$
$$\mathrm{\therefore\:𝑥(𝑡) = 𝑥_{𝑒}(𝑡)\:\:\:\:\:\: … (3)}$$
因此，三角傅立葉級數係數由下式給出：
$$\mathrm{𝑎_{0}\: =\:\frac{1}{𝑇}\int_{-\frac{𝑇}{2}}^{\frac{𝑇}{2}}𝑥(𝑡)\: dt\:=\: \frac{1}{𝑇}\:\int_{-\frac{𝑇}{2}}^{\frac{𝑇}{2}}𝑥_{e}(𝑡)\: dt}$$
$$\mathrm{⇒𝑎_{0}\: =\:\frac{1}{𝑇}(2\int_{0}^{\frac{𝑇}{2}}𝑥_{e}(𝑡) \: dt)\:=\:\frac{2}{𝑇}\int_{0}^{\frac{𝑇}{2}}𝑥(𝑡) \: dt}$$
$$\mathrm{\therefore 𝑎_{0}\: =\:\frac{2}{𝑇}\int_{0}^{\frac{𝑇}{2}}𝑥(𝑡) \: dt\:\:\:.....(4)}$$
係數𝑎𝑛由下式給出：
$$\mathrm{𝑎_{𝑛}\: =\:\frac{2}{𝑇}\int_{-\frac{𝑇}{2}}^{\frac{𝑇}{2}}𝑥(𝑡) \cos\:n\omega_{0}t\: dt\:=\:\frac{2}{𝑇}\int_{-\frac{𝑇}{2}}^{\frac{𝑇}{2}}𝑥_{e}(𝑡) \cos\:n\omega_{0}t\: dt}$$
$$\mathrm{𝑎_{𝑛}\: =\:\frac{2}{𝑇}(2\int_{0}^{\frac{𝑇}{2}}𝑥_{e}(𝑡) \cos\:n\omega_{0}t\: dt)}$$
$$\mathrm{\therefore 𝑎_{𝑛}\: =\:\frac{4}{𝑇}\int_{0}^{\frac{𝑇}{2}}𝑥(𝑡) \cos\:n\omega_{0}t\: dt\:\:\:.....(5)}$$
係數𝑏𝑛由下式給出：
$$\mathrm{𝑏_{𝑛} =\:\frac{2}{𝑇}\int_{-\frac{𝑇}{2}}^{\frac{𝑇}{2}}𝑥_{e}(𝑡) \sin\:n\omega_{0}t\: dt}$$
由於函式(𝑥𝑒(𝑡) sin 𝑛𝜔0𝑡)是奇函式。
$$\mathrm{\therefore 𝑏_{𝑛}\:=\:\frac{2}{𝑇}\int_{-\frac{𝑇}{2}}^{\frac{𝑇}{2}}𝑥_{e}(𝑡) \sin\:n\omega_{0}t\: dt\:= 0\:\:\:.....(6)}$$
因此，偶週期函式的傅立葉級數展開式只包含常數項和餘弦項。此外，當函式存在偶對稱或映象對稱時，該函式的三角傅立葉級數係數由公式(4)、(5)和(6)給出。
從以上討論可以看出，當函式存在偶對稱性時，三角傅立葉係數𝑏𝑛變為零，從而簡化了計算。
偶函式的性質
- 兩個或多個偶函式之和始終為偶函式。
- 兩個偶函式的乘積始終為偶函式。
- 當向偶函式新增常數時，函式的偶性仍然保持。
瀏覽量2K+
