資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究訊號與系統：週期訊號和非週期訊號
如果一個訊號具有確定的模式並在規則的時間間隔內重複，則稱該訊號為**週期訊號**。而不在規則的時間間隔內重複的訊號則稱為**非週期訊號**。
連續時間週期訊號
當且僅當滿足以下條件時，連續時間訊號 x(t) 被認為是週期性的
𝑥(𝑡 + 𝑇) = 𝑥(𝑡) 對於 − ∞ < 𝑡 < ∞
其中，T 是一個正常數，表示週期訊號的週期。滿足週期訊號定義的最小週期值 (T) 稱為訊號的**基波週期**，用 (𝑇0) 表示。
此外，
𝑥(𝑡 + 𝑚𝑇) = 𝑥(𝑡)
其中，m 是一個整數。這意味著如果定義對於 𝑇 = 𝑇0 成立，那麼對於 𝑇 = 2𝑇0、𝑇 = 3𝑇0 等也成立，其中 𝑇0 是基波週期。因此，基波週期定義了週期訊號 x(t) 一個完整週期的持續時間。
週期訊號的週期的倒數稱為訊號的頻率 (f)，即：
$$\mathrm{f=\frac{1}{T}}$$
由於角頻率由下式給出：
𝜔 = 2𝜋𝑓
$$\mathrm{\therefore 週期,\: T=\frac{2\Pi }{f}}$$
圖 1 顯示了一些連續時間週期訊號的示例。
離散時間週期訊號
如果離散時間訊號 x(n) 滿足以下條件，則稱其為週期性的
𝑥(𝑛) = 𝑥(𝑛 + 𝑁); 對於所有整數 𝑛
這裡，N 是週期訊號的週期，且為正整數。滿足上述條件的最小週期值 (N) 稱為訊號的基波週期。基波週期 (N) 可以定義為訊號重複自身所需的最小樣本數。
離散時間週期序列的角頻率由下式給出：
$$\mathrm{\omega =\frac{2\Pi }{N}}$$
因此，序列的週期為：
$$\mathrm{N =\frac{2\Pi }{\omega }}$$
圖 2 顯示了一些離散時間週期序列的示例。
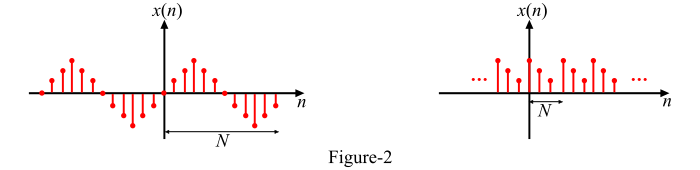
連續時間非週期訊號
如果連續時間訊號沒有確定的模式，並且不在規則的時間間隔內重複，則稱為連續時間**非週期訊號**。
**換句話說**，對於任何時間 t 值都不滿足週期性條件的訊號 x(t) 稱為**非週期訊號**。
圖 3 顯示了一些連續時間非週期訊號的示例。
離散時間非週期訊號
如果對於離散時間訊號 x(n) 的一個 n 值，週期性條件都不滿足，則該離散時間訊號為非週期訊號。圖 4 顯示了一些離散時間非週期訊號的示例。
數值示例
檢查以下訊號是否為週期訊號？如果是週期訊號，則確定訊號的基波週期。
𝑥(𝑡) = sin 10𝜋𝑡
𝑥(𝑡) = sin 𝜋𝑡 𝑢(𝑡)
解答
給定訊號為：
𝑥(𝑡) = sin 10𝜋𝑡
由於訊號 x(t) 是正弦訊號，因此它是一個週期訊號。
現在，將 x(t) 與標準訊號 sin 𝜔𝑡 進行比較，得到：
𝜔 = 10𝜋
$$\mathrm{\therefore \: 基波週期 ,T =\frac{2\Pi }{\omega }=\frac{2\Pi }{10\Pi }=\frac{1}{5}\: 秒}$$給定訊號為：
𝑥(𝑡) = sin 𝜋𝑡 𝑢(𝑡)
這裡，x(t) 是正弦訊號 (sin 𝜋𝑡) 和單位階躍訊號 (𝑢(𝑡)) 的乘積。眾所周知，訊號 sin 𝜋𝑡 是週期訊號，週期為 𝑇 = 2𝜋⁄𝜔，而訊號 𝑢(𝑡) 僅在 0 < 𝑡 < ∞ 存在。因此，𝑢(𝑡) 不是週期訊號。
因此，訊號 x(t) 是一個非週期訊號。
43K+ 瀏覽量
