資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究訊號與系統：訊號的加法和減法
連續時間訊號的加法和減法
兩個連續時間訊號𝑥1(𝑡)和𝑥2(𝑡)的和可以透過在每個時刻將它們的值相加得到。類似地，兩個連續時間訊號𝑥1(𝑡)和𝑥2(𝑡)的差可以透過在每個時刻從另一個訊號（例如𝑥1(𝑡)）中減去一個訊號（例如𝑥2(𝑡)）的值得到。
訊號的加法
如圖 1 所示，設有兩個連續時間訊號𝑥1(𝑡)和𝑥2(𝑡)。這兩個訊號的和𝑥1(𝑡) + 𝑥2(𝑡)也如圖 1 所示。
說明
這兩個訊號的和可以透過考慮不同的時間間隔得到，如下所示：
對於0 ≤ 𝒕 ≤ 1− 𝑥1(𝑡) = 3，而𝑥2(𝑡)從 0 線性增加到 2。因此，和[即，𝑥1(𝑡) + 𝑥2(𝑡)]也將從（3 + 0 = 3）線性增加到（3 + 2 = 5）。
對於1 ≤ 𝒕 ≤ 3− 𝑥1(𝑡) = 2，而𝑥2(𝑡) = 2，因此
𝑥1(𝑡) +𝑥2(𝑡) = 2 + 2 = 4
對於3≤ 𝒕 ≤ 4− 𝑥1(𝑡) = 3，而𝑥2(𝑡)從 2 線性減小到 0。因此，訊號的和也將從（3 + 2 = 5）線性下降到（3 + 0 = 3）。
訊號的減法
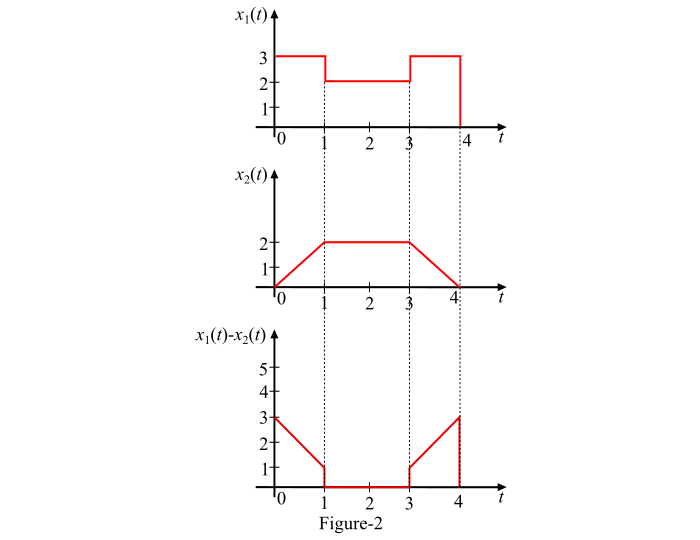
圖 2 顯示了兩個連續時間訊號𝑥1(𝑡)和𝑥2(𝑡)的減法[𝑥1(𝑡) − 𝑥2(𝑡)]。
說明
可以透過考慮不同的時間間隔得到兩個連續時間訊號𝑥1(𝑡)和𝑥2(𝑡)的差，如下所示：
對於0 ≤ 𝒕 ≤ 1−𝑥1(𝑡) = 3，而𝑥2(𝑡)從 0 線性增加到 2。因此，差[𝑥1(𝑡) −𝑥2(𝑡)]從（3 – 0 = 3）線性下降到（3 – 2 = 1）。
對於1 ≤ 𝒕 ≤ 3− 𝑥1(𝑡) = 2，而𝑥2(𝑡) = 2，因此
𝑥1(𝑡) − 𝑥2(𝑡) = 2 − 2 = 0
對於3≤ 𝒕 ≤ 4− 𝑥1(𝑡) = 3，而𝑥2(𝑡)從 2 線性減小到 0。因此，訊號的差將從（3 – 2 = 1）線性上升到（3 – 0 = 3）。
離散時間訊號的加法和減法
在離散時間情況下，兩個序列𝑥1(𝑛)和𝑥2(𝑛)的和可以透過將相應的樣本值相加得到。類似地，兩個序列𝑥1(𝑛)和𝑥2(𝑛)的差可以透過從另一個訊號的對應樣本中減去一個訊號的每個樣本得到。
假設給出兩個離散時間序列，如下所示：
𝑥1(𝑛) = {2, 1, 3, 5, 2}
𝑥2(𝑛) = {1, 4, 2, 1, −3}
然後，離散時間訊號的加法為：
𝑥1(𝑛) + 𝑥2(𝑛) = {2 + 1, 1 + 4, 3 + 2, 5 + 1, 2 − 3} = {3, 5, 5, 6, −1}
類似地，離散時間訊號的減法為：
𝑥1(𝑛) - 𝑥2(𝑛) = {2 − 1, 1 − 4, 3 − 2, 5 − 1, 2 + 3} = {1, −3, 1, 4, 5}
8K+ 次瀏覽
