資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學訊號與系統 – 訊號的時間尺度變換
什麼是時間尺度變換？
將一個常數乘以訊號的時間軸的過程稱為**訊號的時間尺度變換**。根據常數或比例因子的值，訊號的時間尺度變換可能是時間壓縮或時間擴充套件。訊號的時間尺度變換在資料需要以某種速率輸入並以不同速率輸出時非常有用。
連續時間訊號的時間尺度變換
連續時間訊號 x(t) 的時間尺度變換可以透過用 'αt' 代替函式中的 't' 來實現。數學上，它表示為：
𝑥(𝑡) → 𝑦(𝑡) = 𝑥(𝛼𝑡)
其中，α 是一個常數，稱為比例因子。
如果 α > 1，則訊號的時間被壓縮 α 倍，訊號的時間尺度變換稱為時間壓縮。而如果 α < 1，則訊號的時間被擴充套件 α 倍，時間尺度變換稱為時間擴充套件。
示例
考慮圖 1 所示的連續時間訊號 x(t)。可以看出，訊號 x(t) 在時間區間 t = (-2) 到 t = 0 時線性地從 0 增加到 5，在時間區間 t = 0 到 t = 3 時保持在 5 不變，然後在時間區間 t = 3 到 t = 5 時線性地從 5 減小到 0。
**情況一** – 考慮訊號的時間尺度變換（壓縮）：
𝑥(𝑡) → 𝑦(𝑡) = 𝑥(2𝑡)
由於比例因子 α = 2，即 α > 1，因此發生訊號的時間壓縮，壓縮後的訊號如圖 2 所示。
這裡可以看出，時間壓縮訊號 x(2t) 在時間區間 𝑡 = − (2/2) 到 𝑡 = 0 時線性地從 0 增加到 5，在時間區間 t = 0 到 t = (3/2) 時保持在 5 不變，然後在時間區間 t = (3/2) 到 t = (5/2) 時線性地從 5 減小到 0。
**情況二** – 考慮訊號的時間尺度變換（擴充套件）：
$$\mathrm{x(t)\rightarrow y(t)=x\left ( \frac{t}{2} \right )}$$
在這種情況下，α = (1/2)，即 α < 1，因此訊號的時間擴充套件如圖 3 所示。
在圖 3 中，時間擴充套件訊號 x(t/2) 在時間區間 t = (-2×2) 到 t = 0 時線性地從 0 增加到 5，在時間區間 t = 0 到 t = (3×2) 時保持在 5 不變，然後在時間區間 t = (3×2) 到 t = (5×2) 時線性地從 5 減小到 0。
離散時間序列的時間尺度變換
考慮圖 4 所示的離散時間序列 x(n)。
離散序列的時間尺度變換可以定義為：
𝑥(𝑛) → 𝑦(𝑛) = 𝑥(𝑘𝑛)
**情況一** – 如果 k = 2，則
𝑥(𝑛) → 𝑦(𝑛) = 𝑥(2𝑛)
這裡，k > 1，因此訊號的時間被壓縮。我們可以透過代入不同的 n 值來繪製時間壓縮訊號 y(n)，如圖 5 所示。
𝑛 = 0 → 𝑦(0) = 𝑥(0) = 1
𝑛 = (−1) → 𝑦(−1) = 𝑥(−2) = −2
𝑛 = (−2) → 𝑦(−2) = 𝑥(−4) = 0
𝑛 = 1 → 𝑦(1) = 𝑥(2) = 2
𝑛 = 2 → 𝑦(2) = 𝑥(4) = 0
因此，要繪製訊號 x(2n)，我們必須跳過訊號 x(n) 中的奇數編號樣本。
**情況二** – 如果 k = (1/2)，則
$$\mathrm{x(n)\rightarrow y(n)=x\left ( \frac{n}{2} \right )}$$
由於 k < 1，因此訊號被擴充套件 2 倍。我們可以透過代入不同的 n 值來繪製時間擴充套件訊號 y(n)：
𝑛 = 0 → 𝑦(0) = 𝑥(0) = 1
𝑛 = 2 → 𝑦(2) = 𝑥(1) = 3
𝑛 = 4 → 𝑦(4) = 𝑥(2) = 2
𝑛 = (−2) → 𝑦(−2) = 𝑥(−1) = 3
𝑛 = (−4) → 𝑦(−4) = 𝑥(−2) = 2
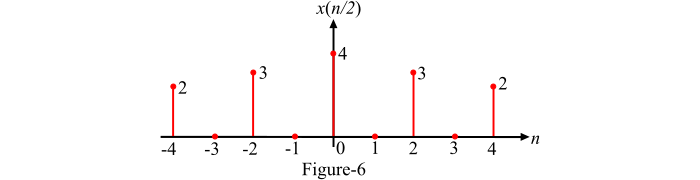
在這種情況下，x(n/2) 中的所有奇數分量都為零，因為訊號 x(n) 在取樣瞬間之間沒有任何值。圖 6 顯示了訊號 $\mathrm{y(n)=x\left ( \frac{n}{2} \right )}$ 的圖。
瀏覽量 18K+
