資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學訊號與系統：實指數訊號與復指數訊號
實指數訊號
指數訊號或指數函式是一個字面意義上表示指數遞增或遞減序列的函式。
連續時間實指數訊號
在每一個時刻都定義的實指數訊號稱為連續時間實指數訊號。連續時間實指數訊號定義如下：
𝑥(𝑡) = 𝐴𝑒𝛼𝑡
其中，A 和 𝛼 都是實數。這裡引數 A 是在 t = 0 時測量的指數訊號的幅度，引數 𝛼 可以是正數或負數。
根據 𝛼 的值，我們得到不同的指數訊號：
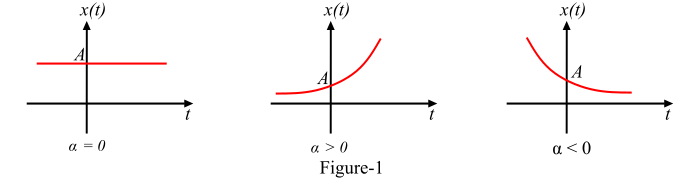
當 𝛼 = 0 時，指數訊號 x(t) 在所有時間都是恆定幅度的訊號。
當 𝛼 > 0，即 𝛼 為正數時，指數訊號 x(t) 是一個增長指數訊號。
當 𝛼 < 0，即 𝛼 為負數時，訊號 x(t) 是一個衰減指數訊號。
這三種訊號的波形如圖 1 所示。
離散時間實指數訊號
在離散時刻定義的實指數訊號稱為離散時間實指數訊號或序列。離散時間實指數序列定義為：
𝑥(𝑛) = 𝑎𝑛 對所有 𝑛
根據 a 的值，離散時間實指數訊號可以是以下型別：
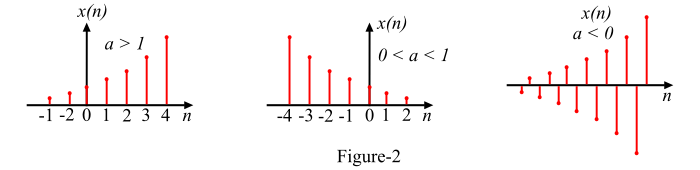
當 a < -1 時，指數序列 x(n) 指數增長。
當 0 < a < 1 時，指數訊號 x(n) 指數衰減。
當 a < 0 時，指數序列 x(n) 具有交替的符號。
這三種訊號在圖 2 中以圖形方式表示。
復指數訊號
樣本為複數（即具有實部和虛部）的指數訊號稱為復指數訊號。
連續時間復指數訊號
連續時間復指數訊號是在每一個時刻都定義的訊號。連續時間覆信號定義為：
𝑥(𝑡) = 𝐴𝑒𝑠𝑡
其中，
A 是訊號的幅度。
s 是一個復變數。
復變數 s 定義為：
𝑠 = 𝜎 + 𝑗𝜔
因此，連續時間複函式也可以寫成
𝑥(𝑡) = 𝐴𝑒(𝜎+𝑗𝜔)𝑡 = 𝐴𝑒𝜎𝑡𝑒𝑗𝜔𝑡
⟹ 𝑥(𝑡) = 𝐴𝑒𝜎𝑡(cos 𝜔𝑡 + 𝑗 sin 𝜔𝑡)
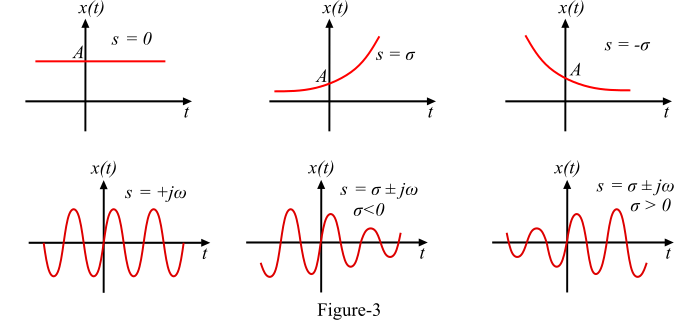
根據 𝜎 和 𝜔 的值，我們得到不同的波形，如圖 3 所示。
離散時間復指數序列
在離散時刻定義的復指數訊號稱為離散時間復指數序列。數學上，離散時間復指數序列定義為：
$$\mathrm{x(n)=a^{n}e^{j(\omega _{0}n+\varphi )}=a^{n}\cos (\omega _{0}n+\varphi)+ja^{n}\sin (\omega _{0}n+\varphi)}$$
根據 a 的大小，我們得到不同型別的離散時間復指數訊號：
對於 |𝑎| = 1，復指數序列的實部和虛部都是正弦的。
對於 |𝑎| > 1，正弦序列的幅度呈指數增長。
對於 |𝑎| < 1，正弦序列的幅度呈指數衰減。
這些訊號的圖形表示如圖 4 所示。
17K+ 次瀏覽
