資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究訊號與系統 – 什麼是半波對稱性？
波形對稱性的重要性
如果一個週期訊號 $x(t)$ 具有某種型別的對稱性，則一些三角傅立葉級數係數可能會變為零，因此係數的計算變得簡單。
半波對稱性
如果一個週期函式 $x(t)$ 滿足以下條件，則稱其具有半波對稱性：
$$\mathrm{x(t)=-x\left ( t ± \frac{T}{2}\right )… (1)}$$
其中，$T$ 是函式的週期。
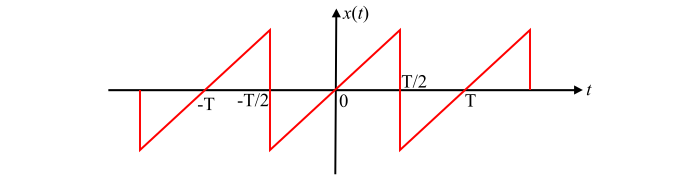
具有半波對稱性的週期函式 $x(t)$ 如圖所示。可以看出，此函式既不是純偶函式也不是純奇函式。對於此類函式，傅立葉展開的直流分量為零，即 $a_{0}=0$。此外，此類函式的傅立葉展開僅包含奇次諧波分量，即 $\omega_{0},3\omega_{0},5\omega_{0},...$ 等。
由於具有半波對稱性的週期函式 $x(t)$ 僅包含奇次諧波項。因此，當 n 為偶數時，$a_{n}=b_{n}=0$。
當 n 為奇數時，係數 $a_{n}$ 和 $b_{n}$ 可以如下確定：
$$\mathrm{a_{n}=\frac{2}{T}\int_{0}^{T}x(t)cos\:n\omega_{0}t\:dt}$$
$$\mathrm{\Rightarrow\:a_{n}=\frac{2}{T}\left [ \int_{0}^{T/2} x(t)cos\:n\omega_{0}t\:dt+\int_{T/2}^{T} x(t)cos\:n\omega_{0}t\:dt\right ]}$$
在第二個積分項中將變數從 $t$ 替換為 $(t+\frac{T}{2})$，我們有：
$$\mathrm{a_{n}=\frac{2}{T}\left [ \int_{0}^{T/2} x(t)cos\:n\omega_{0}t\:dt+ \int_{0}^{T/2} x(t+\frac{T}{2})cos\:n\omega_{0}(t+\frac{T}{2})dt\right ]}$$
根據半波對稱性的定義，即 $x(t)=-x(t ± \frac{T}{2})$，我們有：
$$\mathrm{a_{n}=\frac{2}{T}\int_{0}^{T/2}[x(t)\:cos\:n\omega_{0}t-x(t)\:cos\:n\omega_{0}t\:cos\:n\pi]dt… (2)}$$
因此，具有半波對稱性的函式的傅立葉級數係數 $a_{n}$ 可以定義為：
$$\mathrm{a_{n}=\begin{cases}0; & 當n為偶數時\\frac{4}{T}\int_{0}^{T/2}\:x(t)\:cos\:n\omega_{0}t\:dt\:;& 當n為奇數時\end{cases}}$$
類似地，係數 $b_{n}$ 由下式給出：
$$\mathrm{b_{n}=\begin{cases}0; & 當n為偶數時\\frac{4}{T}\int_{0}^{T/2}\:x(t)\:sin\:n\omega_{0}t\:dt\:;& 當n為奇數時\end{cases}}$$
9K+ 次瀏覽
