兩個同心圓的直徑分別為\( 30 \mathrm{~cm} \)和\( 18 \mathrm{~cm} \)。求與小圓相切的大圓的弦長。

已知

兩個同心圓的直徑分別為\( 30 \mathrm{~cm} \)和\( 18 \mathrm{~cm} \)。

要求

我們要求出與小圓相切的大圓的弦長。

解答

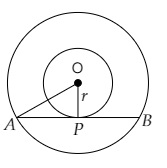
設外圓的半徑為$R$，兩個同心圓中，小圓的半徑為$r$。
$AB$是大圓的弦，並在點$P$處與小圓相切
連線$OP$和$OA$。

這意味著，

$OP\ \perp\ AB$ 且在$P$點平分$AB$。

$OA=R$ 且 $OP=r$

$OA=\frac{30}{2}=15\ cm$，$OP=\frac{18}{2}=9\ cm$

在直角三角形$OAP$中，

$AP=\sqrt{OA^{2}-OP^{2}}$

$=\sqrt{15^{2}-9^{2}}$

$=\sqrt{225-81}$

$=\sqrt{144}$

$=12\ cm$

$AB=2AP$

$=2 \times 12\ cm$

$=24\ cm$

大圓的弦長為24釐米。

教程點

更新於: 2022年10月10日

271 次瀏覽

開啟您的職業生涯

完成課程獲得認證

開始學習