資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究兩個相似三角形的面積分別為 $81\ cm^2$ 和 $49\ cm^2$。求它們對應高的比值。它們對應中線的比值是多少？
已知
兩個相似三角形的面積分別為 $81\ cm^2$ 和 $49\ cm^2$。
要求
我們必須找到它們對應高的比值和它們對應中線的比值。
解
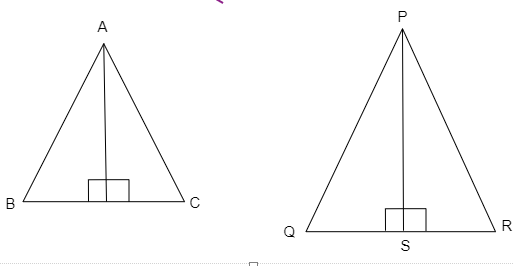
考慮兩個相似三角形，$ΔABC$ 和 $ΔPQR$，$AD$ 和 $PS$ 分別是 $ΔABC$ 和 $ΔPQR$ 的高。
根據相似三角形面積定理，
$\frac{ar(ΔABC)}{ar(ΔPQR)} = \frac{AB^2}{PQ^2}$
$\frac{81}{49} = \frac{AB^2}{PQ^2}$
$ \begin{array}{l}
\frac{AB}{PQ} =\sqrt{\frac{81}{49}}\\
\\
\frac{AB}{PQ} =\frac{9}{7}
\end{array}$
在 $ΔABD$ 和 $ΔPQS$ 中，
$\angle B = \angle Q$
$\angle ABD = \angle PSQ = 90^o$
因此，
$ΔABD ∼ ΔPQS$ (根據角角相似)
$\frac{AB}{PQ} = \frac{AD}{PS}$ (相似三角形的對應邊成比例)
$\frac{AD}{PS} = \frac{9}{7}$
類似地，
兩個相似三角形的面積比等於它們對應中線的平方比。
因此，
高的比值 = 中線的比值 = $\frac{9}{7}$。
更新於: 2022年10月10日
60 次瀏覽
廣告