資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究一座高 30 米的塔的頂部從另一座在同一平面上的塔的底部仰角為 60°，第二座塔的頂部從第一座塔的底部仰角為 30°。求這兩座塔之間的距離。
已知：一座高 30 米的塔的頂部從另一座在同一平面上的塔的底部仰角為 60°，第二座塔的頂部從第一座塔的底部仰角為 30°。
求解：求這兩座塔之間的距離。
解
設兩塔之間的距離為 AB=x 米，另一座塔的高度為 PA=h 米
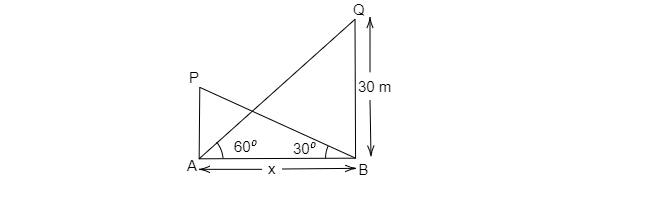
已知塔的高度為 QB=30 米，且∠QAB=60°，∠PBA=30°
現在，在△QAB 中，
tan60°=QB/AB=30/x
⇒√3=30/x
⇒x=30/√3 * √3/√3
⇒x=30√3/3=10√3 米
因此，兩塔之間的距離為 10√3 米。
更新於： 2022-10-10
348 次瀏覽
廣告