AD是等腰三角形ABC的高，其中AB=AC。
(i) 證明AD平分BC
(ii) 證明AD平分∠A。

已知

AD是等腰三角形ABC的高，其中AB=AC。

要求

我們必須證明：
(i) AD平分BC
(ii) AD平分∠A。

解答

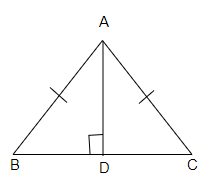
考慮三角形ABD和ACD。

已知AD是三角形ABD和ACD的高。

因此，∠ADB=∠ADC=90°。

我們有AB=AC。

由於AD是公共邊，我們得到：

AD=DA

因此，

我們知道，根據RHS定理，如果一個直角三角形的斜邊和一條直角邊分別等於另一個直角三角形的斜邊和一條直角邊，那麼這兩個直角三角形全等。

因此，

三角形ABD ≅ 三角形ACD

我們也知道，

全等三角形的對應邊相等。

因此，

BD=CD

因此，AD平分BC。

(ii) 同樣，根據全等三角形的對應邊相等：

我們也知道

全等三角形的對應角相等。

因此，

AD平分∠A。

教程點

更新於：2022年10月10日

瀏覽量：57

開啟你的職業生涯

完成課程獲得認證

開始學習