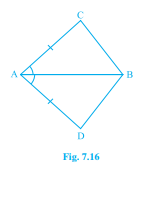
在四邊形\(ACBD\)中，
\(AC=AD\)且\(AB\)平分∠A（見圖7.16）。證明\(△ABC ≅ △ABD\)。
你能對\(BC\)和\(BD\)說什麼？

"64391"

已知

在四邊形ABCD中，AC=AD，AB平分∠A。

要求

我們必須證明△ABC≅△ABD，並說明BC和BD的關係。

解答

讓我們考慮△ABC和△ABD。

已知：

AC=AD

線段AB平分∠A。

因此：

∠CAB=∠DAB

我們知道：

根據邊角邊全等定理

如果兩個三角形的任意一對對應邊及其夾角相等，則這兩個三角形全等。

因此：

△ABC≅△ABD

我們也知道：

全等三角形的對應部分相等：如果兩個三角形全等，則它們的全部對應角和對應邊都必須相等。

這意味著：

BC=BD。

教程點

更新於：2022年10月10日

瀏覽量：57

開啟你的職業生涯

完成課程獲得認證

開始學習