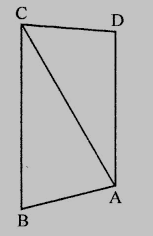
如圖所示，證明
$CD + DA + AB + BC > 2AC$

解題步驟

我們需要證明 $CD + DA + AB + BC > 2AC$。

解答

在給定的圖形中，

$ABCD$ 是一個四邊形，且連線 $AC$。

在 $\triangle ABC$ 中，

$AB + BC > AC$.........…(i) (三角形兩邊之和大於第三邊)

類似地，

在 $\triangle ADC$ 中，

$CD + DA > AC$......…(ii)

將 (i) 和 (ii) 相加，我們得到：

$CD + DA + AB + BC > AC + AC$

$CD + DA + AB + BC > 2AC$。

Tutorialspoint

更新於：2022年10月10日

2AC$.Solution:In the given figure, $ABCD$ is a quadrilateral and $AC$ is joined.In $triangle ABC$,$AB + BC > AC$.........…(i)             (Sum of two sides of a triangle is greater than its third side)Similarly, In $triangle ADC$,$CD + DA >','sharer','toolbar=0,status=0,width=580,height=325');" href="javascript: void(0)" title="分享到Facebook"> 2AC$.Solution:In the given figure, $ABCD$ is a quadrilateral and $AC$ is joined.In $triangle ABC$,$AB + BC > AC$.........…(i)             (Sum of two sides of a triangle is greater than its third side)Similarly, In $triangle ADC$,$CD + DA >','sharer','toolbar=0,status=0,width=580,height=325');" href="javascript: void(0)" title="分享到領英">

40 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習