一個四邊形 $ABCD$ 外接一個圓（見圖）。證明 $AB + CD = AD + BC$。
"

已知：

一個四邊形 $ABCD$ 外接一個圓

要求：

我們必須證明 $AB\ +\ CD\ =\ AD\ +\ BC$。

解答

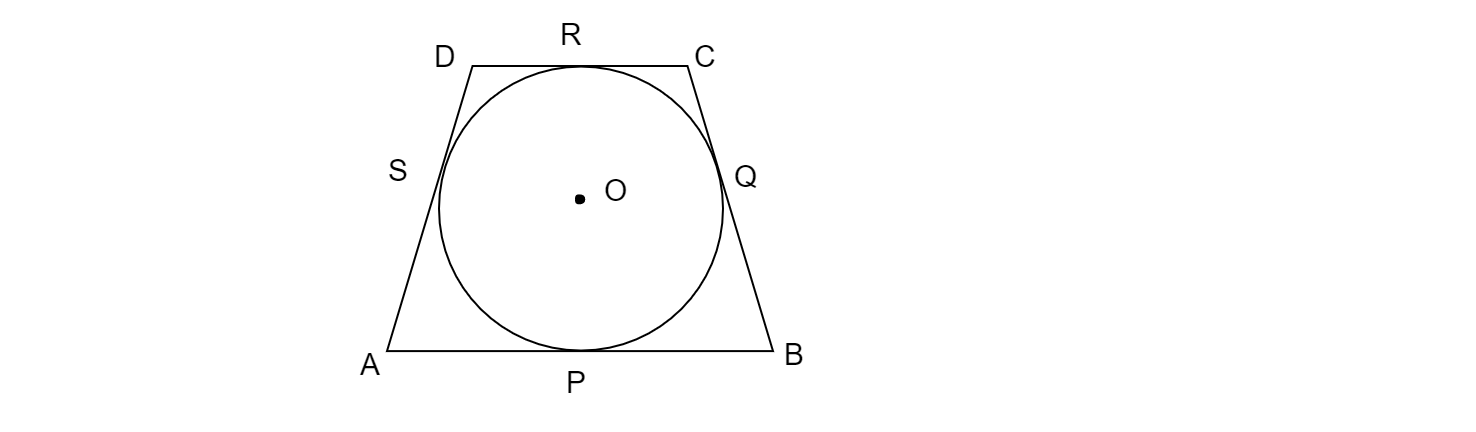
由於從圓外一點引出的切線長度相等，

$AP\ =\ AS\ \dotsc .( 1)$

$BP\ =\ BQ\ \dotsc .( 2)$

$CR\ =\ CQ\ \dotsc .( 3)$

$DR\ =\ DS\ \dotsc .( 4)$

將方程式 $( 1) ,\ ( 2) ,\ ( 3)$ 和 $( 4)$ 相加，得到

$AP\ +\ BP\ +\ CR\ +\ DS\ =\ AS\ +\ BQ\ +\ CQ\ +\ DS$

$\therefore \ ( AP\ +\ BP) \ +\ ( CR\ +\ DR) \ =\ ( AS\ +\ DS) \ +\ ( BQ\ +\ CQ)$

$\therefore \ AB\ +\ CD\ =\ AD\ +\ BC$

證畢。

教程點

更新於: 2022年10月10日

49 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習