已知四邊形$ABCD$是箏形，其中$AB = AD$且$BC = CD$。證明：依次連線各邊中點形成的圖形是矩形。

已知

$ABCD$是箏形，其中$AB = AD$且$BC = CD$。

要求

我們需要證明：依次連線各邊中點形成的圖形是矩形。

解答

設$P, Q, R$和$S$分別是邊$AB, BC, CD$和$DA$的中點。

連線$AC$和$BD$。

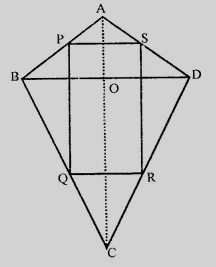
在$\triangle ABD$中，

$P$和$S$分別是$AB$和$AD$的中點。

這意味著，

$PS \parallel BD$且$PS = \frac{1}{2}BD$....…(i)

類似地，

在$\triangle BCD$中，

$Q$和$R$分別是$BC$和$CD$的中點。

這意味著，

$QR \parallel BD$且$QR = \frac{1}{2}BD$...…(ii)

類似地，

$PQ \parallel SR$且$PQ = SR$.....…(iii)

由式(i)、(ii)和(iii)可得，

$PQRS$是平行四邊形。

$AC$和$BD$互相垂直。

因此，

$PQRS$是矩形。

證畢。

教程點

更新於: 2022年10月10日

81 次瀏覽

開啟你的職業生涯

透過完成課程獲得認證

開始學習