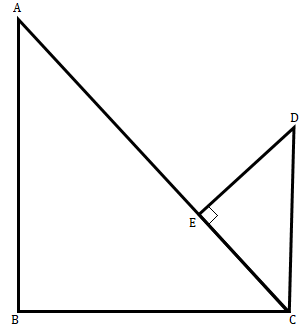
在下圖中，如果$AB\ ⊥\ BC$，$DC\ ⊥\ BC$，並且$DE\ ⊥\ AC$，證明$Δ\ CED\ ∼\ Δ\ ABC$。

已知

在給定圖形中，$AB\ ⊥\ BC$，$DC\ ⊥\ BC$，且$DE\ ⊥\ AC$。

要求

我們必須證明$Δ\ CED\ ∼\ Δ\ ABC$。

解答

在$\vartriangle ABC$和$\vartriangle CED$中，

$\angle BAC+\angle BCA=90^o$

$\angle BCA+\angle ECD=90^o$

這意味著，

$\angle BAC=\angle ECD$

在$\vartriangle ABC$和$\vartriangle CED$中，

$\angle ABC=\angle CED=90^o$

$\angle BAC=\angle ECD$

因此，

$Δ\ CED\ ∼\ Δ\ ABC$。

證畢。

Tutorialspoint

更新於：2022年10月10日

瀏覽量：56

開啟你的職業生涯

完成課程獲得認證

開始學習