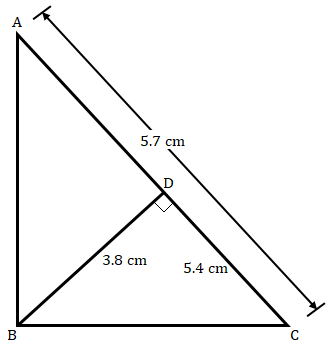
在下圖中，$∠\ ABC\ =\ 90^o$ 且 $BD\ ⊥\ AC$。如果 $AC\ =\ 5.7\ cm$，$BD\ =\ 3.8\ cm$ 且 $CD\ =\ 5.4\ cm$，求 $BC$。
"\n

已知

在給定圖形中，$∠\ ABC\ =\ 90^o$ 且 $BD\ ⊥\ AC$。

$AC\ =\ 5.7\ cm$，$BD\ =\ 3.8\ cm$ 且 $CD\ =\ 5.4\ cm$。

要求

我們必須求 $BC$。

解答

在 $\vartriangle ABC$ 和 $\vartriangle BDC$ 中，

$\angle ABC=\angle BDC=90^o$

$\angle C=\angle C$   (公共角)

因此，

$\vartriangle ABC∼\vartriangle BDC$  (根據角角相似)

$\frac{AB}{BD} = \frac{BC}{DC}$   (相似三角形的對應邊成比例)

$\frac{5.7}{3.8} = \frac{BC}{5.4}$

$BC = \frac{5.7\times 5.4}{3.8}$

$BC = \frac{16.2}{2} = 8.1\ cm$

$BC$ 的度量為 $8.1\ cm$。

教程點

更新時間： 2022 年 10 月 10 日

43 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習