如圖所示，如果$AB \parallel CD$ 且 $CD \parallel EF$，求 $\angle ACE$。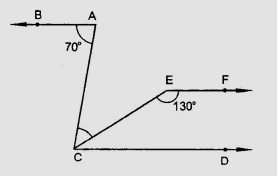"\n

已知

$AB \parallel CD$ 且 $CD \parallel EF$。

要求

我們需要求 $\angle ACE$。

解答

我們知道，

對頂角相等。

同位角相等。

內錯角相等。

同旁內角和為 $180^o$。

因此，

$\angle BAC = 70^o, \angle CEF = 130^o$

$\angle ECD + \angle CEF = 180^o$              (同旁內角)

$\angle ECD + 130^o = 180^o$

$\angle ECD = 180^o - 130^o$

$\angle ECD = 50^o$

$\angle BAC = \angle ACD$                           (內錯角)

$\angle ACD = 70^o$

$\angle ACE = \angle ACD - \angle ECD$

$\angle ACE = 70^o - 50^o$

$\angle ACE = 20^o$

因此，$\angle ACE = 20^o$。

教程點

更新於: 2022年10月10日

80 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

立即開始