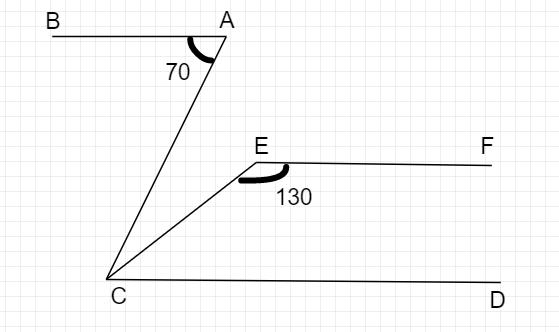
如果 AB||CD 且 CD||EF，求∠ACE
"\n

已知：如果 AB||CD 且 CD||EF 

求解：求∠ACE

解答

EF   和   CD  平行  ;  CE  是穿過平行線  EF   和   CD 的一條橫截線

穿過平行線的橫截線同側內角的和為  180°  

∠DCE  +  ∠CEF   =  180°  

∠ DCE  +  130°   =  180°

∠DCE   =  180°  -   130°

∠DCE   =  50°

AB  平行於 CD

∠BAC  和 ∠ACD  是內錯角。

所以，∠ BAC   =  ∠ACD 

70°   =  ∠ACD 

∠ACD   =  70°

∠ACD   =  ∠DCE  +  ∠ACE 

∠ DCE   =  50°

70°  =  50°  +   ∠ACE

改寫為：

 50°  +  ∠ACE  =  70°

∠ ACE  =  70°  -   50°

 ∠ACE  =   20°

因此，∠ACE 的度數為 20°

Tutorialspoint

更新於: 2022年10月10日

104 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習