如圖所示，$AB \parallel CD \parallel EF$ 且 $GH \parallel KL$。求 $\angle HKL$。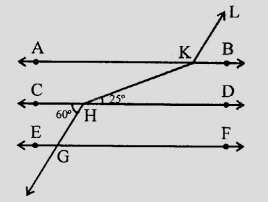"\n

---

已知

$AB \parallel CD \parallel EF$ 且 $GH \parallel KL$。

要求

我們需要求 $\angle HKL$。

解答

延長 $LK$ 和 $GH$

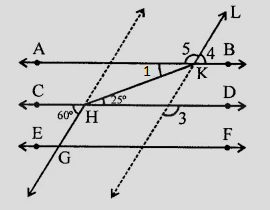
$AB \parallel CD$，$HK$ 是截線。

這意味著，

$\angle 1 = 25^o$                (內錯角)

$\angle 3 = 60^o$                  (同位角)

$\angle 4 = \angle 3 = 60^o$                  (同位角)

$\angle 4 + \angle 5 = 180^o$                  (鄰補角)

$60^o + \angle 5 = 180^o$

$\angle 5 = 180^o - 60^o$

$\angle 5 = 120^o$

因此，

$\angle HKL = \angle 1 + \angle 5$

$ = 25^o + 120^o$

$ = 145^o$

因此，$\angle HKL = 145^o$。