資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會研究
時尚研究
法律研究如圖 10.315 所示，AB∥CD∥EF，且 GH∥KL。求∠HKL 的度數。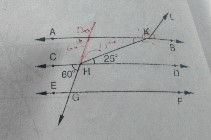
解答
延長直線 GH 到 N，使其與直線 AB 相交於 M
AB∥CD，GM 為截線
⇒∠AMH = ∠CHG = 60° [同位角]
∠NMB = ∠AMH = 60° [對頂角]
AB∥CD，HK 為截線
⇒∠AKH = ∠KHD = 25° [內錯角]
NM∥KL，KM 為截線
⇒∠NMK = ∠LKB = 60° [同位角]
⇒∠LKM = 180° - ∠KLB [鄰補角]
⇒∠LKM = 180° - 60° = 120°
⇒∠HKL = ∠HKA + ∠AKL
⇒∠HKL = 25° + 120° = 145°
更新於：2022年10月10日
瀏覽量：51
廣告