資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究如果一個多項式 $x^4+5x^3+4x^2-10x-12$ 的兩個零點是 $-2$ 和 $-3$，則求其他零點。
已知：多項式 $x^4+5x^3+4x^2-10x-12$ 的兩個零點是 $-2$ 和 $-3$。
求解：求其他零點。
解：
如給定多項式 $x^4+5x^3+4x^2-10x-12$ 的兩個零點是 $-2$ 和 $-3$。
那麼，$( x+2)$ 和 $( x+3)$ 是多項式 $x^4+5x^3+4x^2-10x-12$ 的因式。
令，$g( x)=( x+2)( x+3)=x^2+3x+2x+6$
$\Rightarrow g( x)=x^2+5x+6$
$\because ( x+2)$ 和 $( x+3)$ 是多項式 $x^4+5x^3+4x^2-10x-12$ 的因式。那麼，用 $g( x)=x^2+5x+6$ 除多項式 $x^4+5x^3+4x^2-10x-12$。
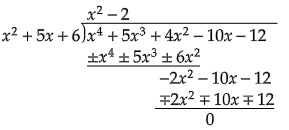
我們得到商 $x^2-2$。因此 $x^2-2$ 也是該多項式的因式。
$\Rightarrow x^2-2=0$
$\Rightarrow x^2=2$
$\Rightarrow x=\pm\sqrt{2}$
因此，$\sqrt{2}$ 和 $-\sqrt{2}$ 是多項式 $x^4+5x^3+4x^2-10x-12$ 的其他零點。
更新於： 2022-10-10
1K+ 次瀏覽
廣告