迴歸技術

---

---

迴歸是一種統計技術，有助於量化相互關聯的經濟變數之間的關係。第一步包括估計自變數的係數，然後衡量估計係數的可靠性。這需要制定假設，並根據假設，我們可以建立一個函式。

如果管理者想要確定公司廣告支出與其銷售收入之間的關係，他將進行假設檢驗。假設更高的廣告支出導致公司更高的銷售額。管理者收集特定時期廣告支出和銷售收入的資料。這個假設可以轉化為數學函式，從而導致：

Y = A + Bx

其中Y是銷售額，x是廣告支出，A和B是常數。

在將假設轉化為函式之後，其基礎是找到因變數和自變數之間的關係。因變數的值對研究人員來說最為重要，並且取決於其他變數的值。自變數用於解釋因變數的變化。它可以分為兩種型別：

• 簡單迴歸 - 一個自變數

• 多元迴歸 - 幾個自變數

簡單迴歸

建立迴歸分析的步驟如下：

• 指定迴歸模型
• 獲取變數資料
• 估計定量關係
• 檢驗結果的統計顯著性
• 將結果用於決策

簡單迴歸公式為：

Y = a + bX + u

Y= 因變數

X= 自變數

a= 截距

b= 斜率

u= 隨機因素

橫截面資料提供關於給定時間一組實體的資訊，而時間序列資料提供關於一個實體隨時間推移的資訊。當我們估計迴歸方程時，它涉及找到因變數和自變數之間最佳線性關係的過程。

普通最小二乘法 (OLS)

普通最小二乘法旨在透過散點擬合一條線，使得點到線的平方偏差之和最小化。這是一種統計方法。通常軟體包執行 OLS 估計。

Y = a + bX

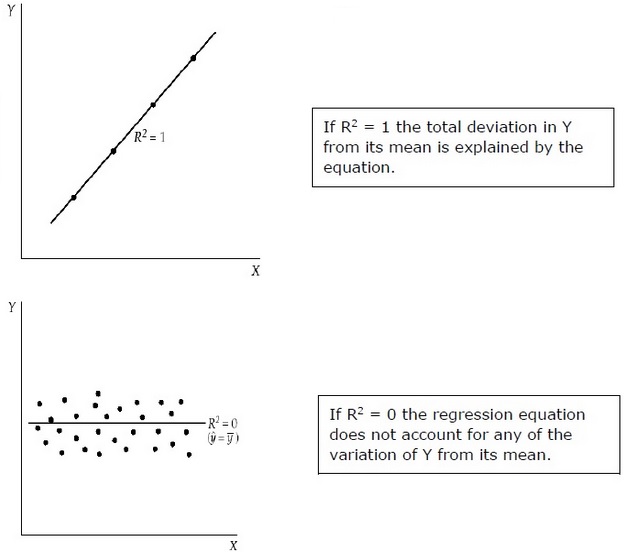
決定係數 (R²)

決定係數是一個衡量指標，它指示因變數變化的百分比是由自變數的變化引起的。R²是模型擬合優度的度量。方法如下：

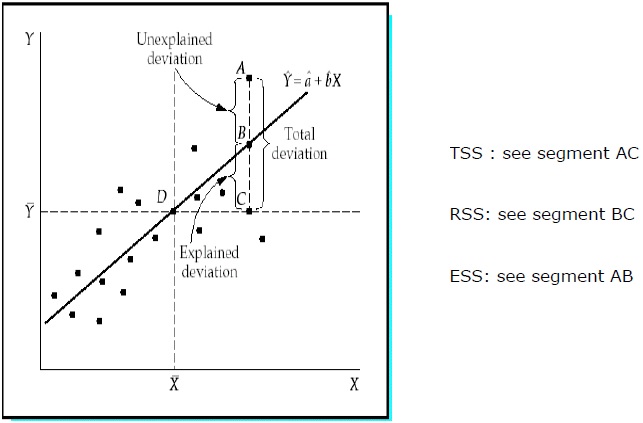
總平方和 (TSS)

Y 的樣本值與其平均值 Y 的平方偏差之和。

TSS = SUM ( Y_i − Y)²

Y_i = 因變數

Y = 因變數的平均值

i = 觀察次數

迴歸平方和 (RSS)

Y 的估計值與其平均值 Y 的平方偏差之和。

RSS = SUM ( Ỷ_i − uY)²

Ỷ_i = Y 的估計值

Y = 因變數的平均值

i = 變異數

誤差平方和 (ESS)

Y 的樣本值與其估計值 Y 的平方偏差之和。

ESS = SUM ( Y_i − Ỷ_i)²

Ỷ_i = Y 的估計值

Y_i = 因變數

i = 觀察次數

R²衡量的是由迴歸模型解釋的 Y 與其平均值總偏差的比例。R²越接近於 1，迴歸方程的解釋力就越大。接近 0 的 R² 表明迴歸方程的解釋力非常小。

為了評估迴歸係數，使用的是來自總體的一個樣本，而不是整個總體。重要的是要根據樣本對總體做出假設，並判斷這些假設有多好。

評估迴歸係數

來自總體的每個樣本都會產生其自身的截距。為了計算統計差異，可以使用以下方法：

雙尾檢驗：

零假設：H₀: b = 0

備擇假設：H_a: b ≠ 0

單尾檢驗：

零假設：H₀: b > 0 (或 b < 0)

備擇假設：H_a: b < 0 (或 b > 0)

統計檢驗：

b = 估計係數

E (b) = b = 0 (零假設)

SE_b = 係數的標準誤

.

t的值取決於自由度、單尾或雙尾檢驗以及顯著性水平。可以使用 t 表來確定t的臨界值。然後將 t 值與臨界值進行比較。如果統計檢驗的絕對值大於或等於臨界 t 值，則需要拒絕零假設。如果統計檢驗的絕對值小於臨界 t 值，則不拒絕零假設。

多元迴歸分析

與簡單迴歸不同，在多元迴歸分析中，係數表示假設其他變數的值保持不變時因變數的變化。

統計顯著性檢驗稱為F 檢驗。F 檢驗很有用，因為它衡量的是整個迴歸方程的統計顯著性，而不僅僅是一個單獨的變數。在這裡，零假設是因變數與總體的自變數之間沒有關係。

公式為：H₀: b1 = b2 = b3 = …. = bk = 0

對於總體，因變數與k個自變數之間不存在關係。

F 檢驗統計量：

$$F \: =\: \frac{ \left ( \frac{R^2}{K} \right )}{\frac{(1-R^2)}{(n-k-1)}}$$

F的臨界值取決於分子和分母自由度以及顯著性水平。可以使用 F 表來確定臨界 F 值。將 F 值與臨界值 (F*) 進行比較：

如果 F > F*，則需要拒絕零假設。

如果 F < F*，則不拒絕零假設，因為因變數與所有自變數之間沒有顯著關係。