傅立葉級數的吉布斯現象

什麼是吉布斯現象？

吉布斯現象是由1848年的亨利·威爾布拉姆發現，之後於1899年由J·威拉德·吉布斯重新發現。

對於具有不連續性的週期訊號，如果透過新增傅立葉級數來重建訊號，則在邊緣周圍會出現過沖。這些過沖以阻尼振盪的方式從邊緣向外衰減。這被稱為吉布斯現象，如下圖所示。

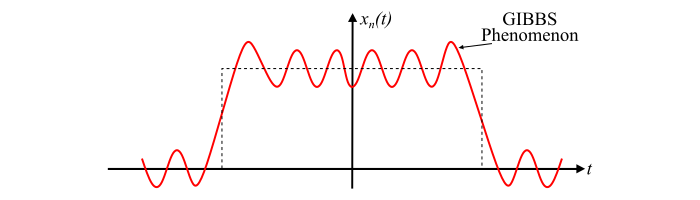
不連續處過沖的幅度與不連續的高度成正比，根據吉布斯，無論傅立葉級數中項數多少，它都約為不連續高度的9%。確切的比例由威爾布拉姆-吉布斯常數給出。

$$\mathrm{\frac{1}{\pi}\int_{0}^{\pi}\frac{sin\:t}{t}dt-\frac{1}{2}= 0.089489 …}$$

還可以注意到，隨著級數中新增的項數增加，頻率增加，過沖變得更尖銳，但相鄰振盪的幅度減小，即，隨著n的增加，原始訊號$x(t)$和截斷訊號$x_{n} (t)$之間的誤差減小，除了邊緣。因此，隨著近似中項數的增加，截斷的傅立葉級數逼近原始訊號$x(t)$。

吉布斯現象的影響

以下是吉布斯現象的一些後果：

• 在訊號處理中，吉布斯現象是不希望的，因為它會導致過沖的削波和振盪的振鈴偽影。

• 在核磁共振成像 (MRI) 中，吉布斯現象會導致相鄰區域具有顯著不同訊號強度時出現偽影。

• 吉布斯現象在影像的離散傅立葉變換中表現出交叉圖案偽影，其中影像在影像的頂部、底部和左側、右側邊界之間具有更尖銳的不連續性。

Manish Kumar Saini

更新於：2021年12月2日

12K+ 瀏覽量

啟動您的職業生涯

完成課程獲得認證

開始學習