資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學指數傅立葉級數係數表示式
指數傅立葉級數
週期訊號可以在一定的時間區間內表示為正交函式的線性組合。如果這些正交函式是指數函式，則稱為指數傅立葉級數。
對於任何週期訊號𝑥(𝑡)，指數形式的傅立葉級數表示為：
$$\mathrm{X(t)=\sum_{n=-\infty}^{\infty}C_n e^{jn\omega_0t}\:\:\:...(1)}$$
其中，𝜔0 = 2𝜋⁄𝑇 是週期函式的角頻率。
指數傅立葉級數的係數
為了計算指數級數的係數，我們將公式 (1) 的兩邊乘以𝑒−𝑗𝑚𝜔0𝑡，並在一個週期內積分，得到：
$$\mathrm{\int_{t_0}^{t_0+T}x(t)e^{-jm\omega_0t}dt=\int_{t_0}^{t_0+T}(\sum_{n=-\infty}^{\infty}C_ne^{jn\omega_0t})e^{-jm\omega_{0}t}dt}$$
$$\mathrm{\Rightarrow\int_{t_0}^{t_0+T}x(t)e^{-jm\omega_0t}dt=\sum_{n=-\infty}^{\infty}C_n\int_{t_0}^{t_0+T}e^{jn\omega_0t}e^{-jm\omega_0t}dt}$$
$$\mathrm{\because \int_{t_0}^{t_0+T}e^{jn\omega_0t}e^{-jm\omega_0t}dt=\begin{cases}0 & m \ne n \\ T & m = n\end{cases}}$$
$$\mathrm{\therefore \int_{t_0}^{t_0+T} x(t)e^{-jm\omega_0t}dt=TC_m}$$
$$\mathrm{\Rightarrow C_m=\frac{1}{T}\int_{t_0}^{(t_0+T)}x(t)e^{-jm\omega_0t}dt}$$
因此，指數傅立葉級數的傅立葉係數𝐶𝑛 為：
$$\mathrm{ C_n=\frac{1}{T}\int_{t_0}^{t_0+T}x(t)e^{-jn\omega_0t}dt\:\:\:....(2)}$$
公式 (2) 也稱為**分析方程**。
此外，指數傅立葉級數的直流分量𝐶0 為：
$$\mathrm{ C_0=\frac{1}{T}\int_{t_0}^{(t_0+T)}x(t)dt\:\:\:....(3)}$$
週期函式 x(t) 的指數傅立葉級數係數只有離散譜，因為係數𝐶𝑛的值僅存在於n的離散值上。由於指數傅立葉級數表示複數譜，因此它具有幅度譜和相位譜。
關於幅度譜和相位譜，需要注意以下幾點：
- 幅度線譜始終是n的偶函式。
- 相位線譜始終是n的奇函式。
數值示例
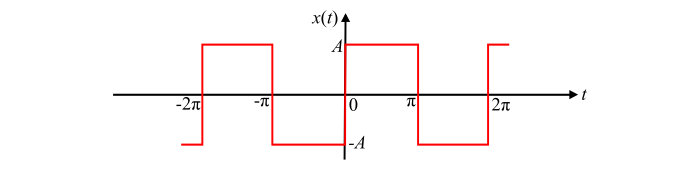
獲得圖中所示波形的指數傅立葉級數。
解答
圖中所示波形表示週期為 T = 2π 的週期函式，其數學表示式為：
$$\mathrm{x(t)=\begin{cases}A & 0 \leq t\leq \pi\\-A & \pi \leq t\leq 2\pi \end {cases}}$$
$$\mathrm{𝑡_0 = 0 \:and \:(𝑡_0 + 𝑇) = 2\pi}$$
這裡，令
因此，該函式的基頻為：
$$\mathrm{\omega_0=\frac{2\pi}{T}=\frac{2\pi}{2\pi}=1}$$
現在，指數傅立葉級數係數𝐶0 為：
$$\mathrm{C_0=\frac{1}{T}\int_{0}^{T}x(t)dt}$$
$$\mathrm{\Rightarrow C_0=\frac{1}{2\pi}\int_{0}^{\pi}A\:dt+\frac{1}{2\pi}\int_{\pi}^{2\pi}-A\:dt=\frac{A}{2\pi}[(t)^{\pi}_{0}-(t)^{2\pi}_{\pi}]=0}$$
同樣，係數𝐶𝑛 為：
$$\mathrm{C_n=\frac{1}{T} \int_{0}^{T}x(t)e^{-jn\omega_0t}dt}$$
$$\mathrm{\Rightarrow C_n=\frac{1}{2\pi} \int_{0}^{\pi}A\:e^{-jnt}dt+\frac{1}{2\pi} \int_{\pi}^{2\pi}-A\:e^{-jnt}dt}$$
$$\mathrm{\Rightarrow C_n=\frac{A}{2\pi}[(\frac{e^{-jnt}}{-jn})^{\pi}_{0}-(\frac{e^{-jnt}}{-jn})^{2\pi}_{\pi}]}$$
$$\mathrm{\Rightarrow C_n=\frac{-A}{j2n\pi}[(e^{-jnt}-e^{0})-(e^{-j2n\pi}-e^{-jn\pi})]}$$
$$\mathrm{\Rightarrow C_n=\frac{-A}{j2n\pi}[\left \{ (-1)^n-1 \right \}-\left \{ 1-(-1)^n \right \}]=-j\frac{2A}{n\pi}}$$
$$\mathrm{\therefore C_n=\begin{cases}0 & n為偶數 \\ -j\frac{2A}{n\pi} & n為奇數 \end {cases}}$$
因此，給定函式的指數傅立葉級數為：
$$\mathrm{x(t)=\sum_{n=-\infty}^{\infty}C_ne^{jn\omega_0t}=\sum_{n=-\infty}^{\infty}-j\frac{2A}{n\pi}e^{jnt};\:n為奇數}$$
13K+ 次瀏覽
