資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學雙邊實指數函式的傅立葉變換
傅立葉變換
連續時間函式$x(t)$的傅立葉變換定義為：
$$\mathrm{X(\omega)=\int_{−\infty}^{\infty}x(t)e^{-j\omega t}dt}$$
雙邊實指數函式的傅立葉變換
設雙邊實指數函式為：
$$\mathrm{x(t)=e^{-a|t|}}$$
雙邊實指數函式定義為：
$$\mathrm{e^{-a|t|}=\begin{cases}e^{at} & t ≤ 0\\e^{-at} & t ≥ 0 \end{cases} =e^{at}u(-t)+e^{-at}u(t) }$$
其中，函式$u(t)$和$u(-t)$分別為單位階躍函式和時間反轉單位階躍函式。
根據傅立葉變換的定義，我們有：
$$\mathrm{X(\omega)=\int_{−\infty}^{\infty}x(t)e^{-j\omega t}dt=\int_{−\infty}^{\infty}e^{-a|t|}e^{-j\omega t}dt}$$
$$\mathrm{\Rightarrow\:X(\omega)=\int_{−\infty}^{\infty}[e^{at}u(-t)+e^{-at}u(t)]e^{-j\omega t}dt}$$
$$\mathrm{\Rightarrow\:X(\omega)=\int_{−\infty}^{0}e^{at}e^{-j\omega t}dt+\int_{0}^{\infty}e^{-at}e^{-j\omega t}dt}$$
$$\mathrm{\Rightarrow\:X(\omega)=\int_{-\infty}^{0}e^{(a-j\omega)t}dt+\int_{0}^{\infty}e^{-(a+j\omega)t}dt}$$
$$\mathrm{\Rightarrow\:X(\omega)=\int_{0}^{\infty}e^{-(a-j\omega)t}dt+\int_{0}^{\infty}e^{-(a+j\omega)t}dt}$$
$$\mathrm{\Rightarrow\:X(\omega)=\left[\frac{e^{-(a-j\omega)t}}{-(a-j\omega)}\right]_{0}^{\infty}+\left[\frac{e^{-(a+j\omega)t}}{-(a+j\omega)}\right]_{0}^{\infty}=\left[\frac{e^{-\infty}-e^{0}}{-(a-j\omega)} \right]+\left[\frac{e^{-\infty}-e^{0}}{-(a+j\omega)} \right]}$$
$$\mathrm{\Rightarrow\:X(\omega)=\frac{1}{a-j\omega}+\frac{1}{a+j\omega}=\frac{2a}{a^{2}+\omega^{2}}}$$
因此，雙邊實指數函式的傅立葉變換為：
$$\mathrm{F[e^{-a|t|}]=X(\omega)=\frac{2a}{a^{2}+\omega^{2}}}$$
或者，也可以表示為：
$$\mathrm{e^{-a|t|}\overset{FT}{\leftrightarrow}\frac{2a}{a^{2}+\omega^{2}}}$$
雙邊實指數函式的傅立葉變換的幅度和相位表示：
$$\mathrm{幅度,\:|X(\omega)|=\frac{2a}{a^{2}+\omega^{2}};\:\:對所有\:\omega}$$
$$\mathrm{相位,\angle X(\omega)=0;\:\:對所有\:\omega}$$
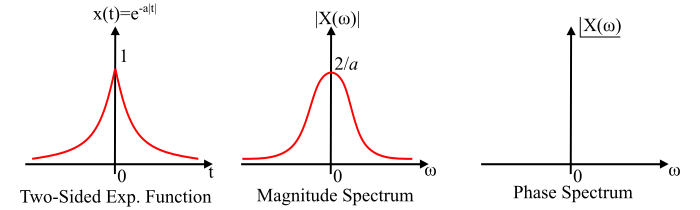
雙邊實指數函式及其幅度和相位譜的圖形表示如圖所示。（此處應插入圖表）
5K+ 瀏覽量
