資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學雙邊和有限持續時間訊號的拉普拉斯變換及其收斂域
什麼是收斂域？
收斂域 (ROC) 定義為 s 平面中函式 $\mathrm{\mathit{x\left ( t \right )}}$ 的拉普拉斯變換收斂的點集。換句話說，函式 𝑋(𝑠) 收斂的 𝑅𝑒(𝑠) (即 𝜎) 的範圍稱為收斂域。
雙邊訊號的 ROC
如果訊號 $\mathrm{\mathit{x\left ( t \right )}}$ 從 -∞ 延伸到 +∞，則稱其為雙邊訊號。雙邊訊號可以表示為兩個不重疊訊號的和，其中一個為右單邊訊號，另一個為左單邊訊號，如圖 1 所示。
對於雙邊訊號，拉普拉斯變換 𝑋(𝑠) 的 ROC 在 s 平面上呈條帶狀，由兩條線 𝜎 = 𝜎r 和 𝜎 = 𝜎 i begrenzt。
數值例子 - 1
求雙邊訊號 $\mathrm{\mathit{x\left ( t \right )\mathrm{=}\mathrm{\mathrm{2}}e^{-\mathrm{3}t}u\left ( t \right )\mathrm{+}\mathrm{3}e^{\mathrm{4}t}u\left ( -t \right )}}$ 的拉普拉斯變換和 ROC。
解答
給定訊號為：
$$\mathrm{\mathit{x\left ( t \right )\mathrm{=}\mathrm{\mathrm{2}}e^{-\mathrm{3}t}u\left ( t \right )\mathrm{+}\mathrm{3}e^{\mathrm{4}t}u\left ( -t \right )}}$$
由於給定訊號是雙邊訊號，訊號 𝑥(𝑡) 的拉普拉斯變換由下式給出：
$$\mathrm{\mathit{L\left [ x\left ( t \right ) \right ]\mathrm{=}\mathrm{2}L\left [ e^{-\mathrm{3}t}u\left ( t \right )\right ]\mathrm{+}\mathrm{3}L\left [ e^{\mathrm{4}t}u\left ( -t \right ) \right ] }}$$
$$\mathrm{\mathit{\Rightarrow X\left ( s \right )\mathrm{=}\frac{\mathrm{2}}{s\mathrm{\mathrm{+}}\mathrm{3}}-\frac{\mathrm{3}}{s-\mathrm{4}};\;\mathrm{ROC} \to Re\left ( s \right )> -\mathrm{3}\: \mathrm{and}\: Re\left ( s \right )< \mathrm{4}}}$$
因此，訊號 $\mathrm{\mathit{x\left ( t \right )}}$ 的拉普拉斯變換的 ROC 為：
$$\mathrm{\mathit{Re\left ( s \right )> -\mathrm{3}\cap Re\left ( s \right )< \mathrm{4}\mathrm{=}-\mathrm{3}< Re\left ( s \right )< \mathrm{4}}}$$
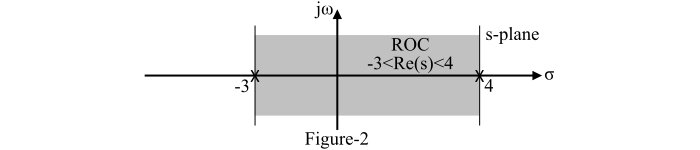
給定訊號 𝑥(𝑡) 的拉普拉斯變換的 ROC 如圖 2 所示。可以看出，給定雙邊訊號的 ROC 在 s 平面上呈條帶狀，位於 s = −3 處的極點右側和 s = +4 處的極點左側。
有限持續時間訊號的 ROC
如果訊號 $\mathrm{\mathit{x\left ( t \right )}}$ 在 $\mathrm{\mathit{t< T_{\mathrm{1}}}}$ 和 $\mathrm{\mathit{t> T_{\mathrm{2}}}}$ 時 $\mathrm{\mathit{x\left ( t \right )}}$ = 0，則稱其為有限持續時間訊號，其中 $\mathrm{\mathit{T_{\mathrm{1}}}}$ 和 $\mathrm{\mathit{T_{\mathrm{2}}}}$ 是某些有限的時間瞬間，如圖 3 所示。
對於絕對可積的有限持續時間訊號，其拉普拉斯變換的 ROC 擴充套件到整個 s 平面。
數值例子 - 2
求圖 4 所示的有限持續時間訊號 $\mathrm{\mathit{x\left ( t \right )}}$ 的拉普拉斯變換和 ROC。
解答
描述給定有限持續時間訊號的方程為：
$$\mathrm{\mathit{x\left ( t \right )\mathrm{=}\left [ u\left ( t-T_{\mathrm{1}} \right )-u\left ( t-T_{\mathrm{2}} \right ) \right ]}}$$
該訊號的兩項都是因果的。該訊號的拉普拉斯變換如下所示：
$$\mathrm{\mathit{L\left [ x\left ( t \right ) \right ]\mathrm{=}L\left [ u\left ( t-T_{\mathrm{1}} \right )\right ]-L\left [ u\left ( t-T_{\mathrm{2}} \right ) \right ] }}$$
$$\mathrm{\mathit{\Rightarrow X\left ( s \right )\mathrm{=}\left ( \frac{e^{-T_{\mathrm{1}}s}}{s}-\frac{e^{-T_{\mathrm{2}}s}}{s} \right )}}$$
$$\mathrm{\mathit{\therefore X\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{s}\left ( {e^{-T_{\mathrm{1}}s}}-{e^{-T_{\mathrm{2}}s}} \right );}\; \; ROC\rightarrow 所有\; \mathit{s}}$$
2K+ 次瀏覽
