資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律對於下列問題，建立二元一次方程組，並用任意代數方法求解
(i) 某寄宿學校的月住宿費包含固定部分和根據就餐天數計算的部分。學生A就餐20天，需支付1000盧比的住宿費；學生B就餐26天，需支付1180盧比的住宿費。求固定費用和每天的就餐費用。
(ii) 一個分數，如果分子減去1，則分數變為$\frac{1}{3}$；如果分母加上8，則分數變為$\frac{1}{4}$。求這個分數。
(iii) 亞什在一項測試中得了40分，每答對一題得3分，每答錯一題扣1分。如果每答對一題得4分，每答錯一題扣2分，那麼亞什將得到50分。測試中共有多少道題？
(iv) A地和B地相距100公里，在同一條公路上。一輛汽車從A地出發，另一輛汽車從B地同時出發。如果兩車沿相同方向行駛，速度不同，則5小時後相遇；如果兩車相向行駛，則1小時後相遇。求這兩輛汽車的速度。
(v) 如果一個矩形的長減少5個單位，寬增加3個單位，則面積減少9平方單位。如果長增加3個單位，寬增加2個單位，則面積增加67平方單位。求矩形的長和寬。
待辦事項
我們需要建立二元一次方程組，並用任意代數方法求解。
解答：(i) 設固定費用和每天的就餐費用分別為$x$和$y$。
當學生A就餐20天時，需支付1000盧比的住宿費。
這意味著，
$x + 20y = 1000$.....(i)
當學生B就餐26天時，需支付1180盧比的住宿費。
這意味著，
$x + 26y = 1180$.....(ii)
用方程(ii)減去方程(i)，得到：
$(x+26y)-(x+20y)=1180-1000$
$x-x+26y-20y=180$
$6y=180$
$y=\frac{180}{6}$
$y=30$
將$y=30$代入方程(i)，得到：
$x+20(30)=1000$
$x+600=1000$
$x=1000-600$
$x=400$
固定費用為400盧比，每天的就餐費用為30盧比。
(ii) 設原分數的分子和分母分別為$x$和$y$。
原分數$=\frac{x}{y}$
如果分子減去1，則分數變為$\frac{1}{3}$。
這意味著，
新分數$=\frac{x-1}{y}$
根據題意，
$\frac{x-1}{y}=\frac{1}{3}$
$3(x-1)=1(y)$ (交叉相乘)
$3x-3=y$
$y=3x-3$.....(i)
如果分母加上8，則分數變為$\frac{1}{4}$。
這意味著，
$\frac{x}{y+8}=\frac{1}{4}$
$4(x)=1(y+8)$ (交叉相乘)
$4x=y+8$
$4x-y-8=0$
$4x-(3x-3)-8=0$ (由(i)得)
$4x-3x+3-8=0$
$x-5=0$
$x=5$
$\Rightarrow y=3(5)-3$
$y=15-3$
$y=12$
因此，原分數為$\frac{5}{12}$。
(iii) 設答對的題數為$x$，答錯的題數為$y$。
這意味著，
總題數$=x+y$。
在第一種情況下，每答對一題得3分，每答錯一題扣1分。
根據題意，
$40=3x+(-1)y$
$y=3x-40$.....(i)
在第二種情況下，每答對一題得4分，每答錯一題扣2分。
根據題意，
$50=4x+(-2)y$
$2y=4x-50$
$2y=2(2x-25)$
$y=2x-25$.....(ii)
由(i)和(ii)得，
$3x-40=2x-25$
$3x-2x=40-25$
$x=15$
這意味著，
$y=2(15)-25$
$y=30-25$
$y=5$
$\Rightarrow x+y=15+5=20$
測試中共有20道題。
(iv) 我們知道，
距離$=$ 速度 $\times$ 時間。
A地和B地之間的距離$= 100\ 公里$。
設從A地出發的第一輛汽車的速度為$x\ 公里/小時$，從B地出發的第二輛汽車的速度為$y\ 公里/小時$。
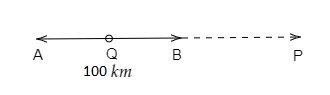
設當兩車沿相同方向行駛時在P點相遇，當兩車相向行駛時在Q點相遇。
當兩車沿相同方向行駛時，5小時後相遇。
第一輛汽車在5小時內行駛的距離$AP= 5\times x\ 公里=5x\ 公里$。
第二輛汽車在5小時內行駛的距離$BP= 5\times y\ 公里=5y\ 公里$。
$AP-BP=100$
$5x-5y=100$
$5(x-y)=5\times20$
$x-y=20$.....(i)
當兩車相向行駛時，1小時後相遇。
第一輛汽車在1小時內行駛的距離$AQ= 1\times x\ 公里=x\ 公里$。
第二輛汽車在1小時內行駛的距離$BQ= 1\times y\ 公里=y\ 公里$。
$AQ+BQ=AB$
$x + y = 100$….(ii)
將方程(i)和(ii)相加，得到：
$x-y+x+y=20+100$
$2x = 120$
$x = \frac{120}{2}$
$x=60$
將$x=60$代入方程(ii)，得到：
$60+y=100$
$y = 100-60$
$y = 40$
因此，第一輛汽車的速度為$60\ 公里/小時$，第二輛汽車的速度為$40\ 公里/小時$。
(v) 設矩形的原長為$l$，原寬為$b$。
原矩形的面積$=lb$。
在第一種情況下，長減少5個單位，寬增加3個單位，矩形的面積減少9平方單位。
新的長$=l-5$
新的寬$=b+3$
新矩形的面積$=(l-5)(b+3)$平方單位
根據題意，
$(l-5)(b+3)=lb-9$
$lb-5b+3l-15=lb-9$
$3l-5b=15-9$
$3l-5b=6$.....(i)
在第二種情況下，長增加3個單位，寬增加2個單位，面積增加67平方單位。
新的長$=l+3$
新的寬$=b+2$
新矩形的面積$=(l+3)(b+2)$平方單位
根據題意，
$(l+3)(b+2)=lb+67$
$lb+2l+3b+6=lb+67$
$2l+3b=67-6$
$2l+3b=61$.....(ii)
用$3\times(ii)$減去$2\times(i)$，得到：
$3(2l+3b)-2(3l-5b)=3(61)-2(6)$
$6l-6l+9b+10b=183-12$
$19b=171$
$b=\frac{171}{19}$
$b=9$
$2l+3(9)=61$ (由(ii)得)
$2l=61-27$
$2l=34$
$l=\frac{34}{2}$
$l=17$
矩形的長為17個單位，寬為9個單位。
瀏覽量：53
