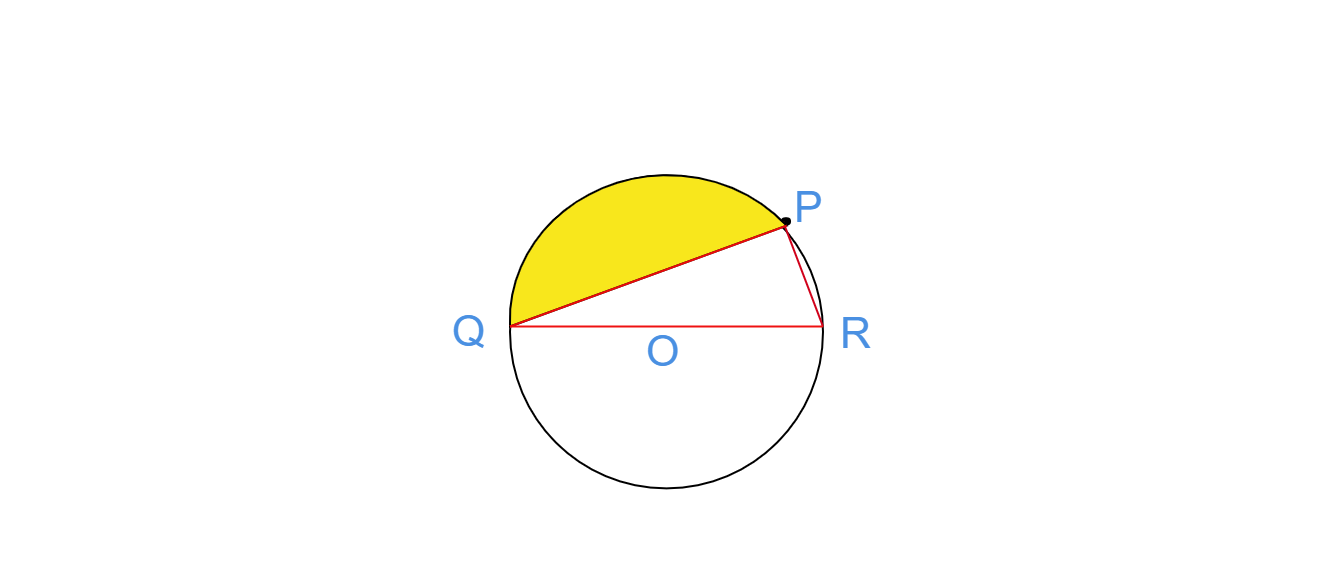
在給定圖形中，求陰影部分的面積，已知 $PQ = 24\ cm，PR = 7\ cm$，且 $O$ 是圓心。
"

已知

在給定圖形中，$PQ=24 cm, PR=7 cm$，且 $O$ 為圓心。

要求

我們需要求陰影部分的面積。

解

陰影部分的面積 = 半圓的面積 - $\triangle PQR$ 的面積

在 $\triangle PQR$ 中，

$\angle QPR = 90°$                [直徑在圓上任何一點所對的角為 $90^o$]

因此，

$QR^2 = PQ^2+PR^2$

$QR^2 = 24^2 + 7^2$

$QR^2 = 576+49$

$QR^2 = 625$

$QR = 25 cm$

直徑 $= 25 cm$

半徑 $r= \frac{25}{2} cm$

三角形的底 (b)$= 7 cm$，高 (h)$= 24cm$。

陰影部分的面積 $= \frac{1}{2} \pi r^2 - \frac{1}{2} \times b \times h$

$= \frac{1}{2}(\pi r^2- b \times h)$

$= \frac{1}{2}( \frac{22}{7}\times \frac{25}{2}\times \frac{25}{2}- 7 \times 24)$

$ = \frac{1}{2}(\frac{13750}{28} - 168)$

$=\frac{1}{2}(491-168)$ 

$= \frac{1}{2}(323)$

$ = \frac{323}{2}$

$= 161.5\ cm^2$.

因此，陰影部分的面積為 $161.5\ cm^2$。

教程點

更新於: 2022年10月10日

98 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習