
其他交流電橋
在上一章中,我們討論了兩種可用於測量電感的交流電橋。在本章中,讓我們討論以下兩種交流電橋。
- Schering電橋
- 維恩電橋
這兩種電橋分別可用於測量電容和頻率。
Schering電橋
Schering電橋是一種具有四個臂的交流電橋,這些臂以菱形或正方形的形式連線,其中一個臂由一個電阻組成,一個臂由電阻和電容的串聯組合組成,一個臂由一個電容組成,另一個臂由電阻和電容的並聯組合組成。
交流檢測器和交流電壓源也用於查詢未知阻抗的值,因此其中一個放置在Schering電橋的一條對角線上,另一個放置在Schering電橋的另一條對角線上。
Schering電橋用於測量電容的值。Schering電橋的電路圖如下所示。
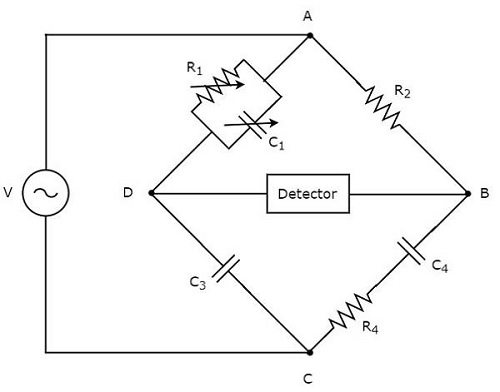
在上圖電路中,AB、BC、CD和DA臂共同構成一個菱形或正方形。AB臂由一個電阻$R_{2}$組成。BC臂由一個電阻$R_{4}$和一個電容$C_{4}$的串聯組合組成。CD臂由一個電容$C_{3}$組成。DA臂由一個電阻$R_{1}$和一個電容$C_{1}$的並聯組合組成。
設$Z_{1}$、$Z_{2}$、$Z_{3}$和$Z_{4}$分別是DA、AB、CD和BC臂的阻抗。這些阻抗的值將為
$Z_{1}=\frac{R_{1}\left ( \frac{1}{j \omega C_{1}} \right )}{R_{1}+\frac{1}{j \omega C_{1}}}$
$\Rightarrow Z_{1}=\frac{R_{1}}{1+j \omega R_{1}C_{1}}$
$Z_{2}=R_{2}$
$Z_{3}=\frac{1}{j \omega C_{3}}$
$Z_{4}=R_{4}+\frac{1}{j \omega C_{4}}$
$\Rightarrow Z_{4}=\frac{1+j \omega R_{4}C_{4}}{j \omega C_{4}}$
代入這些阻抗值到以下交流電橋的平衡條件中。
$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$
$$\frac{1+j \omega R_{4}C_{4}}{j \omega C_{4}}=\frac{R_{2}\left (\frac{1}{j \omega C_{3}} \right )}{\frac{R_{1}}{1+j \omega R_{1}C_{1}}}$$
$\Rightarrow \frac{1+j \omega R_{4}C_{4}}{j \omega C_{4}}=\frac{R_{2}\left ( 1+j \omega R_{1}C_{1} \right )}{j \omega R_{1}C_{3}}$
$\Rightarrow \frac{1+j \omega R_{4}C_{4}}{C_{4}}=\frac{R_{2}\left ( 1+j \omega R_{1}C_{1} \right )}{R_{1}C_{3}}$
$\Rightarrow \frac{1}{C_{4}}+j \omega R_{4}=\frac{R_{2}}{R_{1}C_{3}}+\frac{j\omega C_{1}R_{2}}{C_{3}}$
透過比較上述方程中相應的實部和虛部項,我們將得到
$C_{4}=\frac{R_{1}C_{3}}{R_{2}}$公式1
$R_{4}=\frac{C_{1}R_{2}}{C_{3}}$公式2
透過將$R_{1}$、$R_{2}$和$C_{3}$的值代入公式1,我們將得到電容$C_{4}$的值。類似地,透過將$R_{2}$、$C_{1}$和$C_{3}$的值代入公式2,我們將得到電阻$R_{4}$的值。
Schering電橋的優點是電阻$R_{4}$和電容$C_{4}$的值都與頻率值無關。
維恩電橋
維恩電橋是一種具有四個臂的交流電橋,這些臂以菱形或正方形的形式連線。其中兩個臂由一個電阻組成,一個臂由電阻和電容的並聯組合組成,另一個臂由電阻和電容的串聯組合組成。
為了找到頻率的值,還需要交流檢測器和交流電壓源。因此,這兩個中的一個放置在維恩電橋的一條對角線上,另一個放置在維恩電橋的另一條對角線上。
電路圖如下所示。
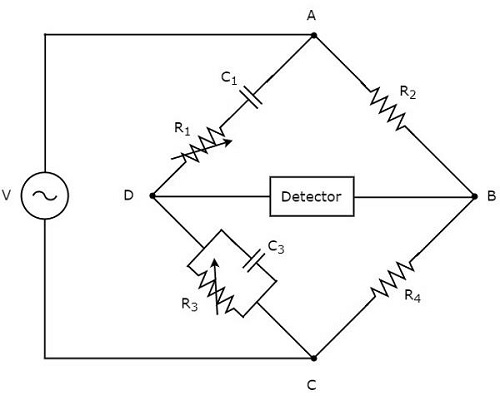
在上圖電路中,AB、BC、CD和DA臂共同構成一個菱形或正方形。AB和BC臂分別由電阻$R_{2}$和$R_{4}$組成。CD臂由一個電阻$R_{3}$和一個電容$C_{3}$的並聯組合組成。DA臂由一個電阻$R_{1}$和一個電容$C_{1}$的串聯組合組成。
設$Z_{1}$、$Z_{2}$、$Z_{3}$和$Z_{4}$分別是DA、AB、CD和BC臂的阻抗。這些阻抗的值將為
$$Z_{1}=R_{1}+\frac{1}{j \omega C_{1}}$$
$$\Rightarrow Z_{1}=\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}$$
$Z_{2}=R_{2}$
$$Z_{3}=\frac{R_{3}\left (\frac{1}{j \omega C_{3}} \right )}{R_{3}+\frac{1}{j \omega C_{3}}}$$
$$\Rightarrow Z_{3}= \frac{R_{3}}{1+j \omega R_{3}C_{3}}$$
$Z_{4}=R_{4}$
代入這些阻抗值到以下交流電橋的平衡條件中。
$$Z_{1}Z_{4}=Z_{2}Z_{3}$$
$$\left (\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}} \right )R_{4}=R_{2}\left (\frac{R_{3}}{1+j \omega R_{3}C_{3}} \right )$$
$\Rightarrow \left (1+j \omega R_{1}C_{1}\right )\left (1+j \omega R_{3}C_{3}\right )R_{4}=j \omega C_{1}R_{2}R_{3}$
$\Rightarrow \left (1+j \omega R_{3}C_{3}+j \omega R_{1}C_{1}-\omega^{2}R_{1}R_{3}C_{1}C_{3}\right )R_{4}=j \omega C_{1}R_{2}R_{3}$
$\Rightarrow R_{4}\left ( \omega^{2}R_{1}R_{3}C_{1}C_{3} \right )+j \omega R_{4}\left (R_{3}C_{3}+R_{1}C_{1} \right )=j \omega C_{1}R_{2}R_{3}$
使上述方程中相應的實部項相等。
$$R_{4}\left (1- \omega^{2}R_{1}R_{3}C_{1}C_{3} \right )=0$$
$\Rightarrow 1- \omega^{2}R_{1}R_{3}C_{1}C_{3} =0$
$\Rightarrow 1= \omega^{2}R_{1}R_{3}C_{1}C_{3}$
$\omega = \frac{1}{\sqrt{R_{1}R_{3}C_{1}C_{3}}}$
代入$\omega = 2 \pi f$到上述方程中。
$$\Rightarrow 2 \pi f= \frac{1}{\sqrt{R_{1}R_{3}C_{1}C_{3}}}$$
$\Rightarrow f= \frac{1}{2 \pi\sqrt{R_{1}R_{3}C_{1}C_{3}}}$
透過將$R_{1}$、$R_{3}$、$C_{1}$和$C_{3}$的值代入上述方程,我們可以找到交流電壓源的頻率$f$的值。
如果$R_{1}=R_{3}=R$且$C_{1}=C_{3}=C$,則我們可以使用以下公式找到交流電壓源的頻率$f$的值。
$$f=\frac{1}{2\pi RC}$$
維恩電橋主要用於查詢AF範圍的頻率值。