直流電流表

---

---

電流是電荷流動的速率。如果這種電荷只沿一個方向流動，則產生的電流稱為直流電（DC）。用於測量直流電的儀器稱為直流電流表。

如果我們將一個電阻與永磁移動線圈（PMMC）檢流計並聯，則整個組合充當直流電流表。直流電流表中使用的並聯電阻也稱為分流電阻或簡稱分流器。為了測量較大值的直流電流，該電阻的值應考慮較小。

直流電流表的電路圖如下所示。

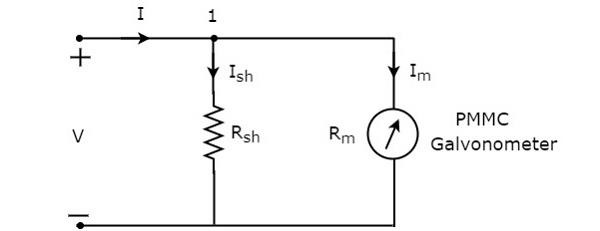
我們必須將此直流電流表與電路分支串聯，以測量要測量的直流電流。並聯連線的元件兩端的電壓相同。因此，分流電阻$R_{sh}$兩端的電壓和檢流計電阻$R_{m}$兩端的電壓相同，因為這兩個元件在上述電路中並聯連線。數學上，可以寫成

$$I_{sh}R_{sh}=I_{m}R_{m}$$

$\Rightarrow R_{sh}=\frac{I_{m}R_{m}}{I_{sh}}$ (公式 1)

節點 1 的基爾霍夫電流定律方程為

$$-I+I_{sh}+I_{m}=0$$

$$\Rightarrow I_{sh}=I-I_{m}$$

代入公式 1 中的$I_{sh}$值。

$R_{sh}=\frac{I_{m}R_{m}}{I-I_{m}}$(公式 2)

在公式 2 右側的分子項中提取$I_{m}$作為公因數

$$R_{sh}=\frac{I_{m}R_{m}}{I_{m}(\frac{1}{I_{m}}-1)}$$

$\Rightarrow R_{sh}=\frac{R_{m}}{\frac{I}{I_{m}}-1}$(公式 3)

其中，

$R_{sh}$為分流電阻

$R_{m}$為檢流計的內阻

$I$為要測量的總直流電流

$I_{m}$為滿刻度偏轉電流

要測量的總直流電流$I$與檢流計的滿刻度偏轉電流$I_{m}$的比率稱為倍率因子，m。數學上，可以表示為

$m=\frac{I}{I_{m}}$(公式 4)

$R_{sh}=\frac{R_{m}}{m-1}$(公式 5)

我們可以根據可用資料使用公式 2 或公式 5 來找到分流電阻的值。

多量程直流電流表

在上一節中，我們討論了透過將電阻與 PMMC 檢流計並聯而獲得的直流電流表。該直流電流表可用於測量特定範圍的直流電流。

如果我們想使用直流電流表測量多個範圍的直流電流，則必須使用多個並聯電阻而不是單個電阻，並且整個電阻組合與 PMMC 檢流計並聯。多量程直流電流表的電路圖如下所示。

將此多量程直流電流表與電路分支串聯，以測量所需範圍的直流電流。透過將開關 s 連線到相應的分流電阻來選擇所需的電流範圍。

令$m_{1}, m_{2}, m_{3}$和$m_{4}$為考慮要測量的總直流電流分別為$I_{1}, I_{2}, I_{3}$和$I_{4}$時直流電流表的倍率因子。以下是對應於每個倍率因子的公式。

$$m_{1}=\frac{I_{1}}{I_{m}}$$

$$m_{2}=\frac{I_{2}}{I_{m}}$$

$$m_{3}=\frac{I_{3}}{I_{m}}$$

$$m_{4}=\frac{I_{4}}{I_{m}}$$

在上圖電路中，有四個分流電阻，$R_{sh1}, R_{sh2}, R_{sh2}$和$R_{sh4}$。以下是對應於這四個電阻的公式。

$$R_{sh1}=\frac{R_{m}}{m_{1}-1}$$

$$R_{sh2}=\frac{R_{m}}{m_{2}-1}$$

$$R_{sh3}=\frac{R_{m}}{m_{3}-1}$$

$$R_{sh4}=\frac{R_{m}}{m_{4}-1}$$

以上公式將幫助我們找到每個分流電阻的阻值。