直流電橋

直流電橋只能使用直流電壓訊號進行操作。直流電橋用於測量橋路中未知電阻的值。惠斯通電橋是直流電橋的一個例子。

現在，讓我們討論一下惠斯通電橋，以找到未知電阻的值。

惠斯通電橋

惠斯通電橋是一種簡單的直流電橋，主要有四個臂。這四個臂形成菱形或正方形，每個臂包含一個電阻。

為了找到未知電阻的值，我們需要檢流計和直流電壓源。因此，這兩個中的一個放置在惠斯通電橋的一個對角線上，另一個放置在惠斯通電橋的另一個對角線上。

惠斯通電橋用於測量中等電阻的值。惠斯通電橋的電路圖如下所示。

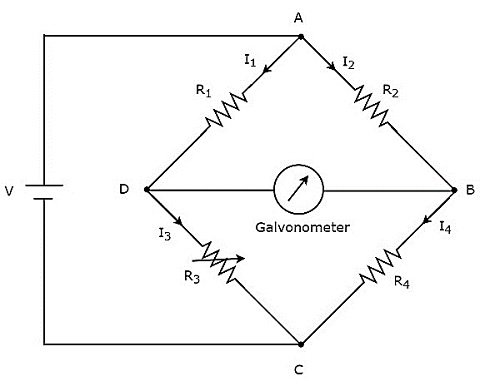
在上面的電路中，臂AB、BC、CD和DA共同形成菱形或正方形。它們分別包含電阻$R_{2}$、$R_{4}$、$R_{3}$和$R_{1}$。設流過這些電阻臂的電流分別為$I_{2}$、$I_{4}$、$I_{3}$和$I_{1}$，這些電流的方向如圖所示。

對角線臂DB和AC分別包含檢流計和V伏的直流電壓源。這裡，電阻$R_{3}$是一個標準的可變電阻，電阻$R_{4}$是一個未知電阻。我們可以透過改變電阻$R_{3}$的阻值來平衡電橋。

當沒有電流流過對角線臂DB時，上述橋路電路處於平衡狀態。這意味著，當電橋平衡時，檢流計沒有偏轉。

當滿足以下兩個條件時，電橋將處於平衡狀態。

• 臂AD上的電壓等於臂AB上的電壓。即

$$V_{AD}=V_{AB}$$

$\Rightarrow I_{1}R_{1}=I_{2}R_{2}$公式1

• 臂DC上的電壓等於臂BC上的電壓。即

$$V_{DC}=V_{BC}$$

$\Rightarrow I_{3}R_{3}=I_{4}R_{4}$公式2

根據以上兩個平衡條件，我們將得到以下兩個結論。

• 流過臂AD的電流將等於臂DC的電流。即

$$I_{1}=I_{3}$$

• 流過臂AB的電流將等於臂BC的電流。即

$$I_{2}=I_{4}$$

取公式1和公式2的比率。

$\frac{I_{1}R_{1}}{I_{3}R_{3}}=\frac{I_{2}R_{2}}{I_{4}R_{4}}$公式3

在公式3中代入$I_{1}=I_{3}$和$I_{2}=I_{4}$。

$$\frac{I_{3}R_{1}}{I_{3}R_{3}}=\frac{I_{4}R_{2}}{I_{4}R_{4}}$$

$$\Rightarrow \frac{R_{1}}{R_{3}}=\frac{R_{2}}{R_{4}}$$

$$\Rightarrow R_{4}=\frac{R_{2}R_{3}}{R_{1}}$$

透過將已知電阻$R_{1}$、$R_{2}$和$R_{3}$的值代入上式，我們將得到電阻$R_{4}$的值。