直流電壓表

---

---

直流電壓表是一種測量儀器，用於測量電路任意兩點間的直流電壓。如果我們將一個電阻器與永久磁鐵移動線圈（PMMC）檢流計串聯，則整個組合共同作用構成直流電壓表。

直流電壓表中使用的串聯電阻也稱為串聯倍率電阻或簡稱為倍率電阻。它主要限制流過檢流計的電流，以防止儀表電流超過滿刻度偏轉值。直流電壓表的電路圖如下所示。

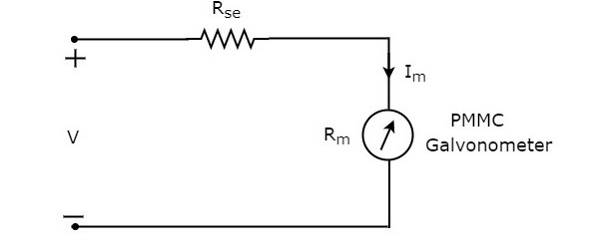
我們必須將此直流電壓表置於電路的兩個點之間，以測量直流電壓。

應用基爾霍夫電壓定律 (KVL)於上述電路的迴路。

$V-I_{m}R_{se}-I_{m}R_{m}=0$ (公式1)

$$\Rightarrow V-I_{m}R_{m}=I_{m}R_{se}$$

$$\Rightarrow R_{se}=\frac{V-I_{m}R_{m}}{I_{m}}$$

$\Rightarrow R_{se}=\frac{V}{I_{m}}-R_{m}$ (公式2)

其中：

$R_{se}$ 為串聯倍率電阻

$V$ 為待測直流電壓的滿量程值

$I_{m}$ 為滿刻度偏轉電流

$R_{m}$ 為檢流計的內阻

待測直流電壓滿量程值 $V$ 與檢流計上的直流電壓降 $V_{m}$ 的比值稱為倍率，m。數學表示式為：

$m=\frac{V}{V_{m}}$ (公式3)

由公式1，我們可以得到待測直流電壓滿量程值 $V$ 的以下公式：

$V=I_{m}R_{se}+I_{m}R_{m}$ (公式4)

檢流計上的直流電壓降 $V_{m}$ 是滿刻度偏轉電流 $I_{m}$ 和檢流計內阻 $R_{m}$ 的乘積。數學表示式為：

$V_{m}=I_{m}R_{m}$ (公式5)

將公式4和公式5代入公式3。

$$m=\frac{I_{m}R_{se}+I_{m}R_{m}}{I_{m}R_{m}}$$

$\Rightarrow m=\frac{R_{se}}{R_{m}}+1$

$\Rightarrow m-1=\frac{R_{se}}{R_{m}}$

$R_{se}=R_{m}\left (m-1 \right )$(公式6)

我們可以根據現有資料使用公式2或公式6來計算串聯倍率電阻的值。

多量程直流電壓表

在上一節中，我們討論了透過將倍率電阻與PMMC檢流計串聯而獲得的直流電壓表。此直流電壓表可用於測量特定範圍的直流電壓。

如果我們想使用直流電壓表測量多個範圍的直流電壓，則必須使用多個並聯倍率電阻代替單個倍率電阻，並且整個電阻組合與PMMC檢流計串聯。電路圖如下所示。

我們必須將此多量程直流電壓表置於電路的兩個點之間，以測量所需範圍的直流電壓。我們可以透過將開關s連線到相應的倍率電阻來選擇所需的電壓範圍。

設 $m_{1},m_{2}, m_{3}$ 和 $m_{4}$ 為當我們將待測直流電壓的滿量程值分別考慮為 $V_{1} , V_{2}, V_{3}$ 和 $V_{4}$ 時直流電壓表的倍率。以下是每個倍率的對應公式。

$$m_{1}=\frac{V_{1}}{V_{m}}$$

$$m_{2}=\frac{V_{2}}{V_{m}}$$

$$m_{3}=\frac{V_{3}}{V_{m}}$$

$$m_{4}=\frac{V_{4}}{V_{m}}$$

在上圖電路中，有四個串聯倍率電阻，$R_{se1}, R_{se2}, R_{se3}$ 和 $R_{se4}$。以下是與這四個電阻對應的公式。

$$R_{se1}=R_{m}\left (m_{1}-1 \right )$$

$$R_{se2}=R_{m}\left (m_{2}-1 \right )$$

$$R_{se3}=R_{m}\left (m_{3}-1 \right )$$

$$R_{se4}=R_{m}\left (m_{4}-1 \right )$$

因此，我們可以使用上述公式求出每個串聯倍率電阻的阻值。