
交流電橋
本章我們將討論交流電橋,它可以用來測量電感。交流電橋僅使用交流電壓訊號工作。交流電橋的電路圖如下所示。
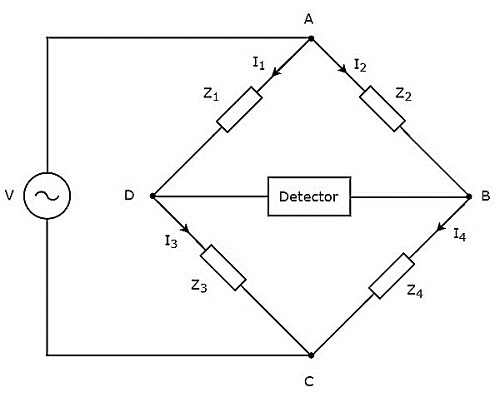
如上圖所示,交流電橋主要由四個臂組成,它們以菱形或正方形連線。所有這些臂都包含一些阻抗。
為了找到未知阻抗的值,還需要檢測器和交流電壓源。因此,這兩個中的一個放置在交流電橋的一個對角線上,另一個放置在交流電橋的另一個對角線上。惠斯通電橋的平衡條件為:
$$R_{4}=\frac{R_{2}R_{3}}{R_{1}}$$
只需在上述等式中用Z代替R,即可得到交流電橋的平衡條件。
$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$
$\Rightarrow Z_{1}Z_{4}=Z_{2}Z_{3}$
這裡,$Z_{1}$和$Z_{2}$是固定阻抗。而$Z_{3}$是標準可變阻抗,$Z_{4}$是未知阻抗。
注意 - 我們可以根據應用選擇四個阻抗中的任意兩個作為固定阻抗,一個阻抗作為標準可變阻抗,另一個阻抗作為未知阻抗。
以下是兩個可以用來測量電感的交流電橋。
- 麥克斯韋電橋
- 海氏電橋
現在,讓我們逐一討論這兩個交流電橋。
麥克斯韋電橋
麥克斯韋電橋是一個交流電橋,它有四個臂,以菱形或正方形的形式連線。該電橋的兩個臂由單個電阻組成,一個臂由電阻和電感的串聯組合組成,另一個臂由電阻和電容的並聯組合組成。
使用交流檢測器和交流電壓源來查詢未知阻抗的值。因此,這兩個中的一個放置在麥克斯韋電橋的一個對角線上,另一個放置在麥克斯韋電橋的另一個對角線上。
麥克斯韋電橋用於測量中等電感的值。麥克斯韋電橋的電路圖如下所示。

在上圖電路中,AB、BC、CD和DA臂共同構成菱形或正方形。AB和CD臂分別由電阻$R_{2}$和$R_{3}$組成。BC臂由電阻$R_{4}$和電感$L_{4}$的串聯組合組成。DA臂由電阻$R_{1}$和電容$C_{1}$的並聯組合組成。
設$Z_{1}$、$Z_{2}$、$Z_{3}$和$Z_{4}$分別是DA、AB、CD和BC臂的阻抗。這些阻抗的值將是
$$Z_{1}=\frac{R_{1}\left ( \frac{1}{j\omega C_{1}} \right )}{R_{1}+\frac{1}{j\omega C_{1}}}$$
$$\Rightarrow Z_{1}=\frac{R_{1}}{1+j \omega R_{1}C_{1}}$$
$Z_{2}=R_{2}$
$Z_{3}=R_{3}$
$Z_{4}=R_{4}+j \omega L_{4}$
將這些阻抗值代入交流電橋的以下平衡條件。
$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$
$$R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{\left ( {\frac{R_{1}}{1+j \omega R_{1}C_{1}}} \right )}$$
$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}\left (1+j \omega R_{1}C_{1} \right )}{R_{1}}$
$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{R_{1}}+\frac{j \omega R_{1}C_{1}R_{2}R_{3}}{R_{1}}$
$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{R_{1}}+j \omega C_{1}R_{2}R_{3}$
透過比較上述等式的相應實部和虛部項,我們將得到
$R_{4}=\frac{R_{2}R_{3}}{R_{1}}$公式1
$L_{4}=C_{1}R_{2}R_{3}$公式2
透過將電阻$R_{1}$、$R_{2}$和$R_{3}$的值代入公式1,我們將得到電阻$R_{4}$的值。同樣,透過將電容$C_{1}$的值和電阻$R_{2}$和$R_{3}$的值代入公式2,我們將得到電感$L_{4}$的值。
麥克斯韋電橋的優點是電阻$R_{4}$和電感$L_{4}$的值都與頻率無關。
海氏電橋
海氏電橋是麥克斯韋電橋的改進版本,它是透過修改麥克斯韋電橋中由電阻和電容的並聯組合組成的臂為由電阻和電容的串聯組合組成的臂而得到的。
海氏電橋用於測量大電感的值。海氏電橋的電路圖如下所示。
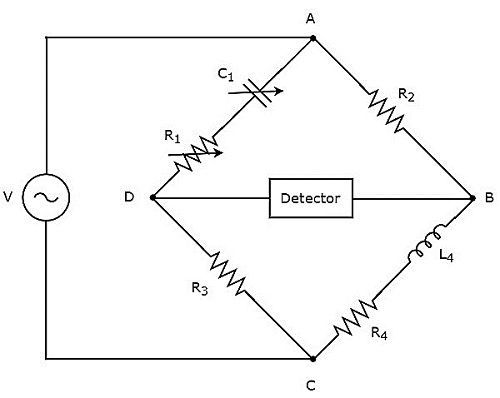
在上圖電路中,AB、BC、CD和DA臂共同構成菱形或正方形。AB和CD臂分別由電阻$R_{2}$和$R_{3}$組成。BC臂由電阻$R_{4}$和電感$L_{4}$的串聯組合組成。DA臂由電阻$R_{1}$和電容$C_{1}$的串聯組合組成。
設$Z_{1}$、$Z_{2}$、$Z_{3}$和$Z_{4}$分別是DA、AB、CD和BC臂的阻抗。這些阻抗的值將是
$$Z_{1}=R_{1}+\frac{1}{j \omega C_{1}}$$
$\Rightarrow Z_{1}=\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}$
$Z_{2}=R_{2}$
$Z_{3}=R_{3}$
$Z_{4}=R_{4}+j \omega L_{4}$
將這些阻抗值代入交流電橋的以下平衡條件。
$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$
$R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}}{\left ( \frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}\right )}$
$R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}j \omega C_{1}}{\left ( 1+j \omega R_{1}C_{1}\right )}$
將上述等式右邊項的分子和分母都乘以$1 - j \omega R_{1}C_{1}$。
$\Rightarrow R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}j \omega C_{1}}{\left ( 1+j \omega R_{1}C_{1}\right )}\times \frac{\left (1 - j \omega R_{1}C_{1} \right )}{\left (1 - j \omega R_{1}C_{1} \right )}$
$\Rightarrow R_{4}+j \omega L_{4}=\frac{\omega^{2}{C_{1}}^{2}R_{1}R_{2}R_{3}+j \omega R_{2}R_{3}C_{1}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )}$
透過比較上述等式的相應實部和虛部項,我們將得到
$R_{4}= \frac{\omega^{2}{C_{1}}^{2}R_{1}R_{2}R_{3}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )}$公式3
$L_{4}= \frac{R_{2}R_{3}C_{1}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )}$公式4
透過將$R_{1}$、$R_{2}$、$R_{3}$、$C_{1}$和$\omega$的值代入公式3和公式4,我們將得到電阻$R_{4}$和電感$L_{4}$的值。