
利薩如圖形
利薩如圖形是在將正弦訊號施加到示波器的水平和垂直偏轉板上時,在螢幕上顯示的圖案。這些圖案將根據施加到示波器水平和垂直偏轉板上的正弦訊號的幅度、頻率和相位差而變化。
下圖顯示了示例利薩如圖形。
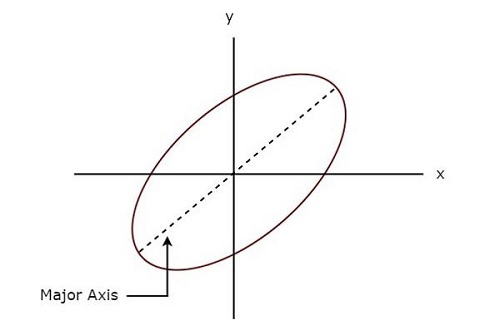
上面的利薩如圖形為橢圓形,其長軸與正x軸有一定的傾角。
使用利薩如圖形進行測量
我們可以從利薩如圖形中進行以下兩種測量。
- 正弦訊號的頻率
- 兩個正弦訊號之間的相位差
現在,讓我們逐一討論這兩種測量方法。
頻率測量
當將正弦訊號施加到示波器的水平和垂直偏轉板上時,螢幕上將顯示利薩如圖形。因此,將具有標準已知頻率的正弦訊號施加到示波器的水平偏轉板上。同樣,將頻率未知的正弦訊號施加到示波器的垂直偏轉板上。
設$f_{H}$和$f_{V}$分別是施加到示波器水平和垂直偏轉板上的正弦訊號的頻率。$f_{H}$和$f_{V}$之間的關係可以用數學表示如下。
$$\frac{f_{V}}{f_{H}}=\frac{n_{H}}{n_{V}}$$
從上述關係式,我們可以得到施加到示波器垂直偏轉板上的正弦訊號的頻率為
$f_{V}=\left ( \frac{n_{H}}{n_{V}} \right )f_{H}$(公式1)
其中,
$n_{H}$是水平切點數
$n_{V}$是垂直切點數
我們可以從利薩如圖形中找到$n_{H}$和$n_{V}$的值。因此,將$n_{H}$、$n_{V}$和$f_{H}$的值代入公式1,我們將得到$f_{V}$的值,即施加到示波器垂直偏轉板上的正弦訊號的頻率。
相位差測量
當將具有相同幅度和頻率的正弦訊號施加到示波器的水平和垂直偏轉板上時,螢幕上會顯示利薩如圖形。
對於一些基於其形狀的利薩如圖形,我們可以直接說出兩個正弦訊號之間的相位差。
如果利薩如圖形是與正x軸成$45^{\circ}$角的直線,則兩個正弦訊號之間的相位差為$0^{\circ}$。這意味著這兩個正弦訊號之間沒有相位差。
如果利薩如圖形是與正x軸成$135^{\circ}$角的直線,則兩個正弦訊號之間的相位差為$180^{\circ}$。這意味著這兩個正弦訊號反相。
如果利薩如圖形為圓形,則兩個正弦訊號之間的相位差為$90^{\circ}$或$270^{\circ}$。
當利薩如圖形為橢圓形時,我們可以使用公式計算兩個正弦訊號之間的相位差。
如果橢圓形利薩如圖形的長軸與正x軸的傾角在$0^{\circ}$和$90^{\circ}$之間,則兩個正弦訊號之間的相位差為:
$$\phi =\sin ^{-1}\left ( \frac{x_{1}}{x_{2}} \right )=\sin ^{-1}\left ( \frac{y_{1}}{y_{2}} \right )$$
如果橢圓形利薩如圖形的長軸與正x軸的傾角在$90^{\circ}$和$180^{\circ}$之間,則兩個正弦訊號之間的相位差為:
$$\phi =180 - \sin ^{-1}\left ( \frac{x_{1}}{x_{2}} \right )=180 - \sin ^{-1}\left ( \frac{y_{1}}{y_{2}} \right )$$
其中,
$x_{1}$是橢圓形利薩如圖形與x軸交點到原點的距離
$x_{2}$是橢圓形利薩如圖形垂直切線到原點的距離
$y_{1}$是橢圓形利薩如圖形與y軸交點到原點的距離
$y_{2}$是橢圓形利薩如圖形水平切線到原點的距離
在本章中,我們學習瞭如何使用公式從利薩如圖形中找到未知正弦訊號的頻率以及兩個正弦訊號之間的相位差。