
- 大資料分析教程
- 大資料分析 - 首頁
- 大資料分析 - 概述
- 大資料分析 - 特徵
- 大資料分析 - 資料生命週期
- 大資料分析 - 架構
- 大資料分析 - 方法論
- 大資料分析 - 核心交付成果
- 大資料採用與規劃注意事項
- 大資料分析 - 關鍵利益相關者
- 大資料分析 - 資料分析師
- 大資料分析 - 資料科學家
- 大資料分析有用資源
- 大資料分析 - 快速指南
- 大資料分析 - 資源
- 大資料分析 - 討論
大資料分析 - 時間序列分析
時間序列是由按日期或時間戳索引的分類或數值變數的一系列觀察值組成。股票價格的時間序列就是一個時間序列資料的典型例子。在下表中,我們可以看到時間序列資料的基本結構。在本例中,每小時記錄一次觀察值。
| 時間戳 | 股票價格 |
|---|---|
| 2015-10-11 09:00:00 | 100 |
| 2015-10-11 10:00:00 | 110 |
| 2015-10-11 11:00:00 | 105 |
| 2015-10-11 12:00:00 | 90 |
| 2015-10-11 13:00:00 | 120 |
通常,時間序列分析的第一步是繪製序列,這通常使用折線圖完成。
時間序列分析最常見的應用是使用資料的時序結構預測數值變數的未來值。這意味著,使用可用的觀測值來預測未來的值。
資料的時序排序意味著傳統的迴歸方法沒有用。為了構建穩健的預測,我們需要考慮資料時序排序的模型。
時間序列分析最廣泛使用的模型稱為自迴歸移動平均 (ARMA)。該模型由兩部分組成,自迴歸 (AR) 部分和移動平均 (MA) 部分。該模型通常稱為ARMA(p, q) 模型,其中p 是自迴歸部分的階數,q 是移動平均部分的階數。
自迴歸模型
AR(p) 讀作 p 階自迴歸模型。數學上寫成 -
$$X_t = c + \sum_{i = 1}^{P} \phi_i X_{t - i} + \varepsilon_{t}$$
其中 {φ1, …, φp} 是要估計的引數,c 是一個常數,隨機變數 εt 表示白噪聲。對引數的值需要一些約束,以便模型保持平穩。
移動平均
MA(q) 表示 q 階移動平均模型 -
$$X_t = \mu + \varepsilon_t + \sum_{i = 1}^{q} \theta_i \varepsilon_{t - i}$$
其中 θ1, ..., θq 是模型的引數,μ 是 Xt 的期望值,εt, εt − 1, ... 是白噪聲誤差項。
自迴歸移動平均
ARMA(p, q) 模型結合了 p 個自迴歸項和 q 個移動平均項。數學上,該模型用以下公式表示 -
$$X_t = c + \varepsilon_t + \sum_{i = 1}^{P} \phi_iX_{t - 1} + \sum_{i = 1}^{q} \theta_i \varepsilon_{t-i}$$
我們可以看到,ARMA(p, q) 模型是AR(p) 和MA(q) 模型的組合。
為了對模型有一些直觀的理解,可以認為方程的 AR 部分試圖估計 Xt − i 觀測值的引數,以便預測變數 Xt 的值。最終它是過去值的加權平均。MA 部分使用相同的方法,但使用先前觀測值的誤差 εt − i。所以最終,模型的結果是一個加權平均值。
以下程式碼片段演示瞭如何在 R 中實現ARMA(p, q)。
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)
繪製資料通常是第一步,以瞭解資料中是否存在時間結構。從圖中我們可以看到,每年年底都有強烈的峰值。
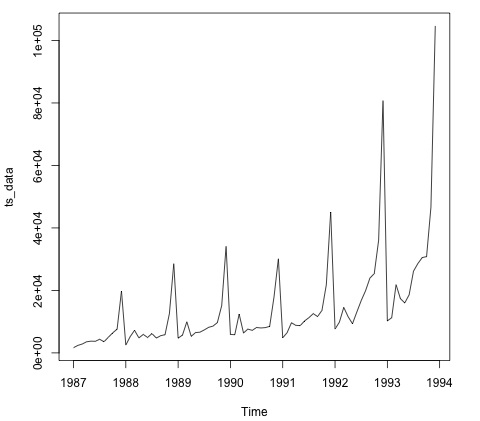
以下程式碼將 ARMA 模型擬合到資料。它運行了幾個模型組合,並選擇誤差最小的那個。
# Fit the ARMA model fit = auto.arima(ts_data) summary(fit) # Series: ts_data # ARIMA(1,1,1)(0,1,1)[12] # Coefficients: # ar1 ma1 sma1 # 0.2401 -0.9013 0.7499 # s.e. 0.1427 0.0709 0.1790 # # sigma^2 estimated as 15464184: log likelihood = -693.69 # AIC = 1395.38 AICc = 1395.98 BIC = 1404.43 # Training set error measures: # ME RMSE MAE MPE MAPE MASE ACF1 # Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172