
- 大資料分析教程
- 大資料分析 - 首頁
- 大資料分析 - 概述
- 大資料分析 - 特徵
- 大資料分析 - 資料生命週期
- 大資料分析 - 架構
- 大資料分析 - 方法論
- 大資料分析 - 核心交付成果
- 大資料採用與規劃考慮
- 大資料分析 - 主要利益相關者
- 大資料分析 - 資料分析師
- 大資料分析 - 資料科學家
- 大資料分析有用資源
- 大資料分析 - 快速指南
- 大資料分析 - 資源
- 大資料分析 - 討論
大資料分析 - 快速指南
大資料分析 - 概述
在過去十年中,需要處理的資料量激增到難以想象的程度,與此同時,資料儲存的成本也系統性地降低了。私營公司和研究機構捕獲了關於使用者互動、業務、社交媒體以及來自行動電話和汽車等裝置感測器的海量資料。這個時代的挑戰在於理解這片資料海洋。這就是大資料分析發揮作用的地方。
大資料分析主要涉及從不同來源收集資料,對其進行整理,使其能夠被分析人員使用,最終交付對組織業務有用的資料產品。

將從不同來源獲取的大量非結構化原始資料轉換為對組織有用的資料產品,構成了大資料分析的核心。
大資料分析 - 資料生命週期
傳統資料探勘生命週期
為了提供一個框架來組織組織所需的工作並從大資料中提取清晰的見解,將其視為一個具有不同階段的週期非常有用。它絕不是線性的,這意味著所有階段彼此相關。這個週期與CRISP方法論中描述的更傳統的資料探勘週期具有表面上的相似性。
CRISP-DM方法論
CRISP-DM方法論代表跨行業標準資料探勘流程,是一個描述資料探勘專家用來解決傳統BI資料探勘問題中常用方法的迴圈。它仍在傳統BI資料探勘團隊中使用。
請檢視下圖。它顯示了CRISP-DM方法論描述的迴圈的主要階段以及它們之間是如何相互關聯的。
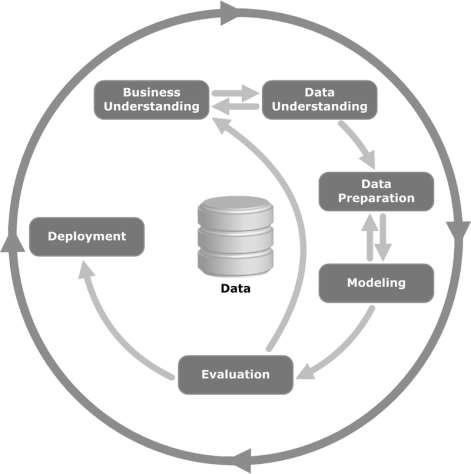
CRISP-DM於1996年構思,次年作為歐盟在ESPRIT資助計劃下的一個專案啟動。該專案由五家公司牽頭:SPSS、Teradata、戴姆勒股份公司、NCR公司和OHRA(一家保險公司)。該專案最終被整合到SPSS中。該方法論極其注重如何詳細指定資料探勘專案。
現在讓我們更深入地瞭解CRISP-DM生命週期中涉及的每個階段:
業務理解 - 此初始階段側重於從業務角度理解專案目標和需求,然後將此知識轉化為資料探勘問題定義。設計初步計劃以實現目標。可以使用決策模型,特別是使用決策模型和符號標準構建的模型。
資料理解 - 資料理解階段從初始資料收集開始,並繼續進行活動,以便熟悉資料,識別資料質量問題,發現對資料的初步見解,或檢測有趣的子集以形成隱藏資訊的假設。
資料準備 - 資料準備階段涵蓋所有活動,以從初始原始資料構建最終資料集(將饋送到建模工具的資料)。資料準備任務很可能多次執行,並且不按任何規定的順序執行。任務包括表、記錄和屬性選擇,以及為建模工具轉換和清理資料。
建模 - 在此階段,選擇和應用各種建模技術,並將其引數校準到最佳值。通常,對於相同的資料探勘問題型別,有多種技術。一些技術對資料形式有特殊要求。因此,通常需要回到資料準備階段。
評估 - 在專案的這個階段,您已經構建了一個(或多個)從資料分析角度來看似乎具有高質量的模型。在繼續進行模型的最終部署之前,務必徹底評估模型並審查構建模型所執行的步驟,以確保它能夠正確實現業務目標。
一個關鍵目標是確定是否存在尚未充分考慮的重要業務問題。在本階段結束時,應就使用資料探勘結果做出決定。
部署 - 模型的建立通常不是專案的結束。即使模型的目的是增加對資料的瞭解,獲得的知識也需要以對客戶有用的方式進行組織和呈現。
根據需求,部署階段可以像生成報告一樣簡單,也可以像實現可重複的資料評分(例如,細分分配)或資料探勘過程一樣複雜。
在許多情況下,將是客戶而不是資料分析師執行部署步驟。即使分析師部署了模型,客戶也需要預先了解需要執行哪些操作才能實際使用建立的模型。
SEMMA方法論
SEMMA是SAS為資料探勘建模開發的另一種方法論。它代表Sample(抽樣)、Explore(探索)、Modify(修改)、Model(建模)和Asses(評估)。以下是其各個階段的簡要說明:
抽樣 - 該過程從資料抽樣開始,例如,選擇用於建模的資料集。資料集應足夠大,包含足夠的資訊來檢索,但又足夠小以高效使用。此階段還處理資料分割槽。
探索 - 此階段涵蓋透過發現變數之間預期和意外的關係以及異常值(藉助資料視覺化)來理解資料。
修改 - 修改階段包含用於選擇、建立和轉換變數以準備資料建模的方法。
建模 - 在建模階段,重點是將各種建模(資料探勘)技術應用於準備好的變數,以便建立可能提供所需結果的模型。
評估 - 對建模結果的評估顯示了建立模型的可靠性和實用性。
CRISM-DM和SEMMA的主要區別在於,SEMMA側重於建模方面,而CRISP-DM更重視建模之前的週期階段,例如理解要解決的業務問題,理解和預處理將用作輸入的資料(例如,機器學習演算法)。
大資料生命週期
在當今大資料環境中,以前的方法要麼不完整,要麼次優。例如,SEMMA方法論完全忽略了不同資料來源的資料收集和預處理。這些階段通常構成成功大資料專案的大部分工作。
大資料分析週期可以透過以下階段來描述:
- 業務問題定義
- 研究
- 人力資源評估
- 資料採集
- 資料清洗
- 資料儲存
- 探索性資料分析
- 資料準備建模和評估
- 建模
- 實施
在本節中,我們將對大資料生命週期的這些階段進行一些闡述。
業務問題定義
這是傳統BI和大資料分析生命週期中的一個共同點。通常,定義問題並正確評估它可能為組織帶來的潛在收益,是大資料專案的一個非平凡階段。提及這一點似乎顯而易見,但必須評估專案的預期收益和成本。
研究
分析其他公司在相同情況下所做的事情。這包括尋找對您的公司來說合理的解決方案,即使這意味著將其他解決方案適應您的公司擁有的資源和要求。在此階段,應定義未來階段的方法論。
人力資源評估
一旦定義了問題,接下來就合理地分析當前員工是否能夠成功完成專案。傳統的BI團隊可能無法為所有階段提供最佳解決方案,因此在啟動專案之前,應該考慮是否有必要外包專案的一部分或僱傭更多人員。
資料採集
本節是大資料生命週期中的關鍵;它定義了哪些型別的配置檔案將需要交付最終資料產品。資料收集是該過程中的一個非平凡步驟;它通常涉及從不同來源收集非結構化資料。例如,它可能涉及編寫爬蟲程式從網站檢索評論。這涉及處理文字,可能使用不同的語言,通常需要大量時間才能完成。
資料清洗
一旦資料被檢索(例如,從網路),就需要將其儲存在易於使用的格式中。繼續以評論為例,假設資料是從不同的站點檢索的,每個站點的資料顯示方式都不同。
假設一個數據源以星級評定的形式提供評論,因此可以將其讀取為響應變數y ∈ {1, 2, 3, 4, 5}的對映。另一個數據源使用兩個箭頭系統提供評論,一個用於向上投票,另一個用於向下投票。這意味著響應變數的形式為y ∈ {正面,負面}。
為了組合這兩個資料來源,必須做出決定以使這兩個響應表示等效。這可能涉及將第一個資料來源的響應表示轉換為第二種形式,將一顆星視為負面,五顆星視為正面。此過程通常需要大量時間才能高質量地交付。
資料儲存
資料處理完成後,有時需要將其儲存在資料庫中。大資料技術為此提供了多種選擇。最常見的選擇是使用Hadoop檔案系統進行儲存,它為使用者提供了一個有限版本的SQL,稱為Hive查詢語言。從使用者的角度來看,這允許大多數分析任務以與傳統BI資料倉庫中類似的方式完成。其他可考慮的儲存選項包括MongoDB、Redis和SPARK。
這個階段與人力資源的知識有關,具體來說是他們實施不同架構的能力。傳統資料倉庫的修改版本仍在大型應用中使用。例如,Teradata和IBM提供可以處理TB級資料的SQL資料庫;PostgreSQL和MySQL等開源解決方案仍在大型應用中使用。
儘管不同儲存在後臺的工作方式有所不同,但從客戶端來看,大多數解決方案都提供SQL API。因此,深入瞭解SQL仍然是大資料分析的關鍵技能。
這個階段事先似乎是最重要的主題,但實際上並非如此,它甚至不是必需的階段。可以實現一個使用即時資料的大資料解決方案,在這種情況下,我們只需要收集資料來開發模型,然後即時實施它。因此,根本不需要正式儲存資料。
探索性資料分析
一旦資料被清洗並以可以從中檢索洞察資訊的方式儲存,資料探索階段就是強制性的。此階段的目標是理解資料,這通常是透過統計技術和資料繪圖完成的。這是一個評估問題定義是否有意義或是否可行的良好階段。
資料準備建模和評估
此階段涉及重塑先前檢索到的清洗資料,並使用統計預處理進行缺失值插補、異常值檢測、歸一化、特徵提取和特徵選擇。
建模
之前的階段應該已經產生了多個用於訓練和測試的資料集,例如,一個預測模型。此階段涉及嘗試不同的模型,並期待解決手頭的業務問題。實際上,通常希望模型能夠對業務提供一些見解。最後,選擇最佳模型或模型組合,評估其在留出資料集上的效能。
實施
在此階段,開發的資料產品將被部署到公司的數管道中。這涉及在資料產品執行時設定驗證方案,以跟蹤其效能。例如,在實施預測模型的情況下,此階段將涉及將模型應用於新資料,並在響應可用後評估模型。
大資料分析 - 方法論
在方法論方面,大資料分析與傳統的實驗設計統計方法有很大不同。分析始於資料。我們通常以某種方式對資料建模以解釋響應。這種方法的目標是預測響應行為或理解輸入變數如何與響應相關。在統計實驗設計中,通常會開發一個實驗,並由此檢索資料。這允許以統計模型可以使用的方式生成資料,其中某些假設成立,例如獨立性、正態性和隨機性。
在大資料分析中,我們得到了資料。我們無法設計一個滿足我們最喜歡的統計模型的實驗。在大規模應用分析中,大量工作(通常佔80%的努力)僅用於資料清洗,以便機器學習模型可以使用它。
在實際的大規模應用中,我們沒有一個獨特的方法論可以遵循。通常,一旦定義了業務問題,就需要一個研究階段來設計使用方法論。但是,一些通用指南是相關的,並且幾乎適用於所有問題。
大資料分析中最重要的任務之一是**統計建模**,這意味著監督和無監督分類或迴歸問題。一旦資料被清洗和預處理,就可以用於建模,應注意使用合理的損失度量評估不同的模型,然後一旦模型被實施,就應該進一步評估和報告結果。預測建模中一個常見的陷阱是僅僅實施模型而從不衡量其效能。
大資料分析 - 核心交付成果
如大資料生命週期中所述,開發大資料產品產生的資料產品在大多數情況下是以下一些——
**機器學習實現**——這可能是一個分類演算法、一個迴歸模型或一個細分模型。
**推薦系統**——目標是開發一個基於使用者行為推薦選擇的系統。**Netflix**是這種資料產品的典型示例,它根據使用者的評分推薦其他電影。
**儀表盤**——企業通常需要工具來視覺化聚合資料。儀表盤是一種圖形機制,使這些資料可訪問。
**臨時分析**——通常業務領域有一些問題、假設或謬論可以透過對資料進行臨時分析來解答。
大資料分析 - 主要利益相關者
在大公司中,為了成功地開發大資料專案,需要管理層支援該專案。這通常涉及找到一種方法來展示該專案的業務優勢。我們沒有一個獨特的解決方案來尋找專案的贊助商,但下面給出了一些指導方針——
檢查誰以及在哪裡是與您感興趣的專案類似的其他專案的贊助商。
在關鍵管理職位上有私人聯絡會有幫助,因此如果專案有前景,可以啟動任何聯絡。
誰會從您的專案中受益?專案啟動後,您的客戶是誰?
制定一個簡單、清晰且令人興奮的提案,並與您組織中的關鍵參與者分享。
尋找專案贊助商的最佳方法是理解問題以及實施後將產生的資料產品是什麼。這種理解將有助於說服管理層大資料專案的重要性。
大資料分析 - 資料分析師
資料分析師擁有面向報告的個人資料,具有使用SQL從傳統資料倉庫中提取和分析資料的經驗。他們的任務通常是在資料儲存方面或報告一般業務結果方面。
許多組織都在努力尋找市場上合格的資料科學家。然而,選擇未來的資料分析師並教授他們成為資料科學家的相關技能是一個好主意。這絕非易事,通常需要這個人獲得定量領域的碩士學位,但這絕對是一個可行的選擇。合格的資料分析師必須具備的基本技能如下:
- 商業理解
- SQL程式設計
- 報表設計和實施
- 儀表盤開發
大資料分析 - 資料科學家
資料科學家的角色通常與諸如預測建模、開發細分演算法、推薦系統、A/B 測試框架以及經常處理原始非結構化資料等任務相關聯。
他們工作的性質需要對數學、應用統計和程式設計有深入的理解。資料分析師和資料科學家之間有一些共同的技能,例如查詢資料庫的能力。兩者都分析資料,但資料科學家的決策可能會對組織產生更大的影響。
以下是資料科學家通常需要具備的一些技能:
- 使用統計軟體包進行程式設計,例如:R、Python、SAS、SPSS或Julia
- 能夠從不同來源清洗、提取和探索資料
- 統計模型的研究、設計和實施
- 深厚的統計、數學和計算機科學知識
在大資料分析中,人們通常會混淆資料科學家和資料架構師的角色。實際上,區別很簡單。資料架構師定義資料將儲存在其中的工具和架構,而資料科學家則使用此架構。當然,如果需要進行臨時專案,資料科學家應該能夠設定新的工具,但基礎設施的定義和設計不應屬於他的任務。
大資料分析 - 問題定義
在本教程中,我們將開發一個專案。本教程中的每個後續章節都處理迷你專案部分中較大專案的一部分。這被認為是一個應用教程部分,將提供對現實世界問題的瞭解。在這種情況下,我們將從專案的 問題定義 開始。
專案描述
本專案的目標是開發一個機器學習模型,使用求職者的簡歷文字作為輸入來預測他們的每小時薪水。
使用上面定義的框架,很容易定義這個問題。我們可以將 *X = {x1, x2, …, xn}* 定義為使用者的簡歷,其中每個特徵都可以以最簡單的方式表示該單詞出現的次數。然後響應是實值,我們試圖預測個人的每小時美元薪水。
這兩個考慮足以得出結論:提出的問題可以用監督迴歸演算法來解決。
問題定義
**問題定義**可能是大資料分析管道中最複雜和最被忽視的階段之一。為了定義資料產品將解決的問題,經驗是強制性的。大多數 aspiring 資料科學家在這個階段幾乎沒有經驗。
大多數大資料問題可以分為以下幾種型別:
- 監督分類
- 監督迴歸
- 無監督學習
- 學習排序
現在讓我們進一步瞭解這四個概念。
監督分類
給定一個特徵矩陣 *X = {x1, x2, ..., xn}*,我們開發一個模型 M 來預測定義為 *y = {c1, c2, ..., cn}* 的不同類別。例如:給定保險公司客戶的交易資料,可以開發一個模型來預測客戶是否會流失。後者是一個二元分類問題,有兩個類別或目標變數:流失和未流失。
其他問題涉及預測多個類別,我們可能對進行數字識別感興趣,因此響應向量將定義為:*y = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}*,最先進的模型將是卷積神經網路,特徵矩陣將定義為影像的畫素。
監督迴歸
在這種情況下,問題定義與前面的示例非常相似;區別在於響應。在迴歸問題中,響應 y ∈ ℜ,這意味著響應是實值的。例如,我們可以開發一個模型,根據求職者的簡歷內容預測他們的每小時薪水。
無監督學習
管理層常常渴望獲得新的見解。細分模型可以提供這種見解,以便營銷部門為不同的細分市場開發產品。開發細分模型的一個好方法,與其考慮演算法,不如選擇與所需細分相關的特徵。
例如,在電信公司中,按客戶的手機使用情況細分客戶是很有意義的。這將涉及忽略與細分目標無關的特徵,而只包含相關的特徵。在這種情況下,這將選擇諸如每月使用的簡訊數量、呼入和撥出分鐘數等特徵。
學習排序
這個問題可以被認為是一個迴歸問題,但它具有特殊的特點,值得單獨處理。這個問題涉及到給定一個文件集合,我們尋求找到給定查詢的最相關的排序。為了開發一個監督學習演算法,需要標記給定查詢的排序的相關性。
值得注意的是,為了開發監督學習演算法,需要標記訓練資料。這意味著,為了訓練一個模型,例如,從影像中識別數字,我們需要手工標記大量的示例。有一些網路服務可以加快這個過程,並且通常用於此任務,例如亞馬遜Mechanical Turk。事實證明,當提供更多資料時,學習演算法會提高其效能,因此在監督學習中,標記相當數量的示例實際上是強制性的。
大資料分析 - 資料收集
資料收集在大資料週期中扮演著最重要的角色。網際網路為各種主題提供了幾乎無限的資料來源。該領域的重要性取決於業務型別,但傳統行業可以獲取各種外部資料來源,並將其與交易資料相結合。
例如,假設我們想構建一個推薦餐廳的系統。第一步是收集資料,在這種情況下,是從不同的網站收集餐廳評論並將它們儲存在資料庫中。由於我們感興趣的是原始文字,並將使用它進行分析,因此資料儲存位置與開發模型無關。這聽起來可能與大資料主要技術相矛盾,但是為了實現大資料應用程式,我們只需要使其即時執行。
Twitter小型專案
一旦問題被定義,接下來的階段就是收集資料。以下小型專案的想法是致力於從網路上收集資料並將其結構化,以便用於機器學習模型。我們將使用R程式語言從Twitter REST API收集一些推文。
首先建立一個Twitter帳戶,然後按照**twitteR**軟體包vignette中的說明建立一個Twitter開發者帳戶。這是這些說明的摘要:
填寫基本資訊後,轉到“設定”選項卡,然後選擇“讀取、寫入和訪問直接訊息”。
確保在執行此操作後單擊儲存按鈕。
在“詳細資訊”選項卡中,記下您的消費者金鑰和消費者金鑰。
在您的R會話中,您將使用API金鑰和API金鑰值。
最後執行以下指令碼。這將從其在github上的儲存庫安裝**twitteR**軟體包。
install.packages(c("devtools", "rjson", "bit64", "httr"))
# Make sure to restart your R session at this point
library(devtools)
install_github("geoffjentry/twitteR")
我們感興趣的是獲取包含字串“big mac”的資料,並找出哪些主題在此方面脫穎而出。為此,第一步是從Twitter收集資料。以下是我們收集Twitter所需資料的R指令碼。此程式碼也可在bda/part1/collect_data/collect_data_twitter.R檔案中找到。
rm(list = ls(all = TRUE)); gc() # Clears the global environment
library(twitteR)
Sys.setlocale(category = "LC_ALL", locale = "C")
### Replace the xxx’s with the values you got from the previous instructions
# consumer_key = "xxxxxxxxxxxxxxxxxxxx"
# consumer_secret = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# access_token = "xxxxxxxxxx-xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# access_token_secret= "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
# Connect to twitter rest API
setup_twitter_oauth(consumer_key, consumer_secret, access_token, access_token_secret)
# Get tweets related to big mac
tweets <- searchTwitter(’big mac’, n = 200, lang = ’en’)
df <- twListToDF(tweets)
# Take a look at the data
head(df)
# Check which device is most used
sources <- sapply(tweets, function(x) x$getStatusSource())
sources <- gsub("</a>", "", sources)
sources <- strsplit(sources, ">")
sources <- sapply(sources, function(x) ifelse(length(x) > 1, x[2], x[1]))
source_table = table(sources)
source_table = source_table[source_table > 1]
freq = source_table[order(source_table, decreasing = T)]
as.data.frame(freq)
# Frequency
# Twitter for iPhone 71
# Twitter for Android 29
# Twitter Web Client 25
# recognia 20
大資料分析 - 資料清洗
一旦資料被收集,我們通常會有來自不同來源、具有不同特徵的資料。最直接的步驟是使這些資料來源同質化,並繼續開發我們的資料產品。然而,這取決於資料的型別。我們應該問問自己,使資料同質化是否實際。
也許資料來源完全不同,如果對來源進行同質化,資訊丟失將會很大。在這種情況下,我們可以考慮替代方案。一個數據源能否幫助我構建迴歸模型,而另一個數據源構建分類模型?是否可以利用異質性而不是僅僅丟失資訊?做出這些決定是使分析變得有趣和具有挑戰性的原因。
對於評論來說,每個資料來源都可能有一種語言。同樣,我們有兩個選擇:
**同質化** - 這涉及將不同的語言翻譯成我們擁有更多資料的語言。翻譯服務的質量是可以接受的,但是如果我們想使用API翻譯大量資料,成本將非常高。有一些軟體工具可以完成這項任務,但這也會很昂貴。
**異質化** - 是否可以為每種語言開發一種解決方案?由於很容易檢測語料庫的語言,我們可以為每種語言開發一個推薦器。這將涉及更多工作,需要根據可用語言的數量調整每個推薦器,但如果我們只有幾種語言可用,這絕對是一個可行的選擇。
Twitter小型專案
在本例中,我們需要首先清理非結構化資料,然後將其轉換為資料矩陣,以便對其應用主題建模。一般來說,從Twitter獲取資料時,有一些字元我們不感興趣,至少在資料清洗過程的第一階段是這樣。
例如,在獲取推文後,我們得到這些奇怪的字元:“<ed><U+00A0><U+00BD><ed><U+00B8><U+008B>”。這些可能是表情符號,因此為了清理資料,我們將使用以下指令碼將其刪除。此程式碼也可在bda/part1/collect_data/cleaning_data.R檔案中找到。
rm(list = ls(all = TRUE)); gc() # Clears the global environment
source('collect_data_twitter.R')
# Some tweets
head(df$text)
[1] "I’m not a big fan of turkey but baked Mac &
cheese <ed><U+00A0><U+00BD><ed><U+00B8><U+008B>"
[2] "@Jayoh30 Like no special sauce on a big mac. HOW"
### We are interested in the text - Let’s clean it!
# We first convert the encoding of the text from latin1 to ASCII
df$text <- sapply(df$text,function(row) iconv(row, "latin1", "ASCII", sub = ""))
# Create a function to clean tweets
clean.text <- function(tx) {
tx <- gsub("htt.{1,20}", " ", tx, ignore.case = TRUE)
tx = gsub("[^#[:^punct:]]|@|RT", " ", tx, perl = TRUE, ignore.case = TRUE)
tx = gsub("[[:digit:]]", " ", tx, ignore.case = TRUE)
tx = gsub(" {1,}", " ", tx, ignore.case = TRUE)
tx = gsub("^\\s+|\\s+$", " ", tx, ignore.case = TRUE)
return(tx)
}
clean_tweets <- lapply(df$text, clean.text)
# Cleaned tweets
head(clean_tweets)
[1] " WeNeedFeminlsm MAC s new make up line features men woc and big girls "
[1] " TravelsPhoto What Happens To Your Body One Hour After A Big Mac "
資料清洗小型專案的最後一步是擁有經過清理的文字,我們可以將其轉換為矩陣並應用演算法。從儲存在**clean_tweets**向量中的文字中,我們可以輕鬆地將其轉換為詞袋矩陣並應用無監督學習演算法。
大資料分析 - 資料彙總
報告在大資料分析中非常重要。每個組織都必須定期提供資訊來支援其決策過程。這項任務通常由具有SQL和ETL(提取、轉換和載入)經驗的資料分析師處理。
負責這項任務的團隊有責任將大資料分析部門產生的資訊傳播到組織的不同領域。
以下示例演示了資料彙總的含義。導航到資料夾**bda/part1/summarize_data**,並在資料夾內雙擊開啟**summarize_data.Rproj**檔案。然後,開啟**summarize_data.R**指令碼並檢視程式碼,並按照提供的說明進行操作。
# Install the following packages by running the following code in R.
pkgs = c('data.table', 'ggplot2', 'nycflights13', 'reshape2')
install.packages(pkgs)
**ggplot2**軟體包非常適合資料視覺化。**data.table**軟體包是在**R**中進行快速且記憶體高效的彙總的一個不錯的選擇。最近的基準測試表明,它甚至比**pandas**(用於執行類似任務的Python庫)更快。
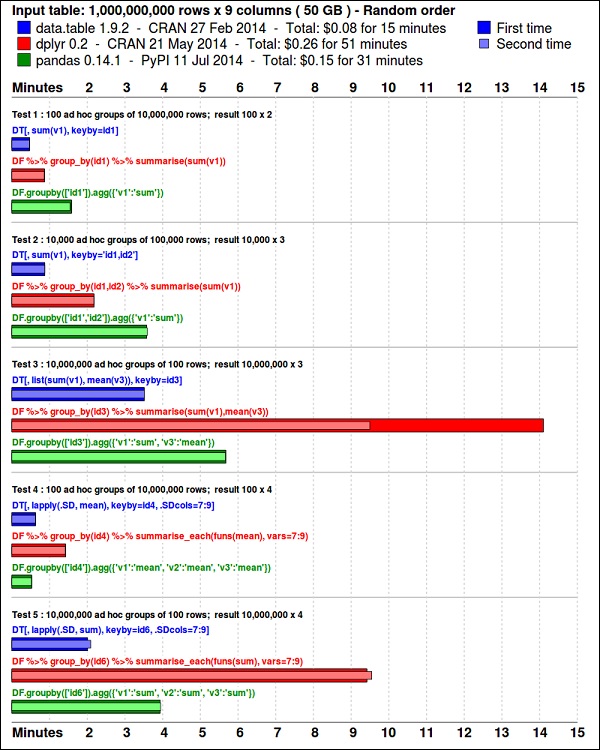
使用以下程式碼檢視資料。此程式碼也可在**bda/part1/summarize_data/summarize_data.Rproj**檔案中找到。
library(nycflights13) library(ggplot2) library(data.table) library(reshape2) # Convert the flights data.frame to a data.table object and call it DT DT <- as.data.table(flights) # The data has 336776 rows and 16 columns dim(DT) # Take a look at the first rows head(DT) # year month day dep_time dep_delay arr_time arr_delay carrier # 1: 2013 1 1 517 2 830 11 UA # 2: 2013 1 1 533 4 850 20 UA # 3: 2013 1 1 542 2 923 33 AA # 4: 2013 1 1 544 -1 1004 -18 B6 # 5: 2013 1 1 554 -6 812 -25 DL # 6: 2013 1 1 554 -4 740 12 UA # tailnum flight origin dest air_time distance hour minute # 1: N14228 1545 EWR IAH 227 1400 5 17 # 2: N24211 1714 LGA IAH 227 1416 5 33 # 3: N619AA 1141 JFK MIA 160 1089 5 42 # 4: N804JB 725 JFK BQN 183 1576 5 44 # 5: N668DN 461 LGA ATL 116 762 5 54 # 6: N39463 1696 EWR ORD 150 719 5 54
以下程式碼包含資料彙總示例。
### Data Summarization # Compute the mean arrival delay DT[, list(mean_arrival_delay = mean(arr_delay, na.rm = TRUE))] # mean_arrival_delay # 1: 6.895377 # Now, we compute the same value but for each carrier mean1 = DT[, list(mean_arrival_delay = mean(arr_delay, na.rm = TRUE)), by = carrier] print(mean1) # carrier mean_arrival_delay # 1: UA 3.5580111 # 2: AA 0.3642909 # 3: B6 9.4579733 # 4: DL 1.6443409 # 5: EV 15.7964311 # 6: MQ 10.7747334 # 7: US 2.1295951 # 8: WN 9.6491199 # 9: VX 1.7644644 # 10: FL 20.1159055 # 11: AS -9.9308886 # 12: 9E 7.3796692 # 13: F9 21.9207048 # 14: HA -6.9152047 # 15: YV 15.5569853 # 16: OO 11.9310345 # Now let’s compute to means in the same line of code mean2 = DT[, list(mean_departure_delay = mean(dep_delay, na.rm = TRUE), mean_arrival_delay = mean(arr_delay, na.rm = TRUE)), by = carrier] print(mean2) # carrier mean_departure_delay mean_arrival_delay # 1: UA 12.106073 3.5580111 # 2: AA 8.586016 0.3642909 # 3: B6 13.022522 9.4579733 # 4: DL 9.264505 1.6443409 # 5: EV 19.955390 15.7964311 # 6: MQ 10.552041 10.7747334 # 7: US 3.782418 2.1295951 # 8: WN 17.711744 9.6491199 # 9: VX 12.869421 1.7644644 # 10: FL 18.726075 20.1159055 # 11: AS 5.804775 -9.9308886 # 12: 9E 16.725769 7.3796692 # 13: F9 20.215543 21.9207048 # 14: HA 4.900585 -6.9152047 # 15: YV 18.996330 15.5569853 # 16: OO 12.586207 11.9310345 ### Create a new variable called gain # this is the difference between arrival delay and departure delay DT[, gain:= arr_delay - dep_delay] # Compute the median gain per carrier median_gain = DT[, median(gain, na.rm = TRUE), by = carrier] print(median_gain)
大資料分析 - 資料探索
**探索性資料分析**是由John Tuckey(1977)提出的一個概念,它代表了統計學的一種新視角。Tuckey的想法是,在傳統的統計學中,資料沒有以圖形方式進行探索,它只是用於檢驗假設。第一次嘗試開發工具是在斯坦福大學進行的,該專案名為prim9。該工具能夠將資料視覺化為九個維度,因此能夠提供資料的多元視角。
近年來,探索性資料分析是必不可少的,並且已被納入大資料分析生命週期。能夠發現見解並能夠在組織中有效地傳達見解的能力,是強大的EDA能力的推動。
基於Tuckey的想法,貝爾實驗室開發了**S程式語言**,以便提供一個互動式介面來進行統計分析。S的想法是提供具有易於使用的語言的廣泛圖形功能。在當今的大資料背景下,基於**S**程式語言的**R**是最流行的分析軟體。

以下程式演示了探索性資料分析的使用。
以下是探索性資料分析的示例。此程式碼也可在**part1/eda/exploratory_data_analysis.R**檔案中找到。
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# Using the code from the previous section
# This computes the mean arrival and departure delays by carrier.
DT <- as.data.table(flights)
mean2 = DT[, list(mean_departure_delay = mean(dep_delay, na.rm = TRUE),
mean_arrival_delay = mean(arr_delay, na.rm = TRUE)),
by = carrier]
# In order to plot data in R usign ggplot, it is normally needed to reshape the data
# We want to have the data in long format for plotting with ggplot
dt = melt(mean2, id.vars = ’carrier’)
# Take a look at the first rows
print(head(dt))
# Take a look at the help for ?geom_point and geom_line to find similar examples
# Here we take the carrier code as the x axis
# the value from the dt data.table goes in the y axis
# The variable column represents the color
p = ggplot(dt, aes(x = carrier, y = value, color = variable, group = variable)) +
geom_point() + # Plots points
geom_line() + # Plots lines
theme_bw() + # Uses a white background
labs(list(title = 'Mean arrival and departure delay by carrier',
x = 'Carrier', y = 'Mean delay'))
print(p)
# Save the plot to disk
ggsave('mean_delay_by_carrier.png', p,
width = 10.4, height = 5.07)
該程式碼應該生成如下所示的影像:
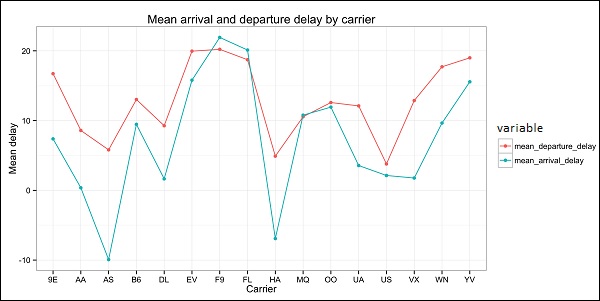
大資料分析 - 資料視覺化
為了理解資料,將其視覺化通常很有用。通常在大資料應用程式中,興趣在於發現見解,而不僅僅是製作漂亮的圖表。以下是使用圖表來理解資料的一些不同方法的示例。
要開始分析航班資料,我們可以首先檢查數值變數之間是否存在相關性。此程式碼也可在**bda/part1/data_visualization/data_visualization.R**檔案中找到。
# Install the package corrplot by running
install.packages('corrplot')
# then load the library
library(corrplot)
# Load the following libraries
library(nycflights13)
library(ggplot2)
library(data.table)
library(reshape2)
# We will continue working with the flights data
DT <- as.data.table(flights)
head(DT) # take a look
# We select the numeric variables after inspecting the first rows.
numeric_variables = c('dep_time', 'dep_delay',
'arr_time', 'arr_delay', 'air_time', 'distance')
# Select numeric variables from the DT data.table
dt_num = DT[, numeric_variables, with = FALSE]
# Compute the correlation matrix of dt_num
cor_mat = cor(dt_num, use = "complete.obs")
print(cor_mat)
### Here is the correlation matrix
# dep_time dep_delay arr_time arr_delay air_time distance
# dep_time 1.00000000 0.25961272 0.66250900 0.23230573 -0.01461948 -0.01413373
# dep_delay 0.25961272 1.00000000 0.02942101 0.91480276 -0.02240508 -0.02168090
# arr_time 0.66250900 0.02942101 1.00000000 0.02448214 0.05429603 0.04718917
# arr_delay 0.23230573 0.91480276 0.02448214 1.00000000 -0.03529709 -0.06186776
# air_time -0.01461948 -0.02240508 0.05429603 -0.03529709 1.00000000 0.99064965
# distance -0.01413373 -0.02168090 0.04718917 -0.06186776 0.99064965 1.00000000
# We can display it visually to get a better understanding of the data
corrplot.mixed(cor_mat, lower = "circle", upper = "ellipse")
# save it to disk
png('corrplot.png')
print(corrplot.mixed(cor_mat, lower = "circle", upper = "ellipse"))
dev.off()
此程式碼生成以下相關矩陣視覺化:
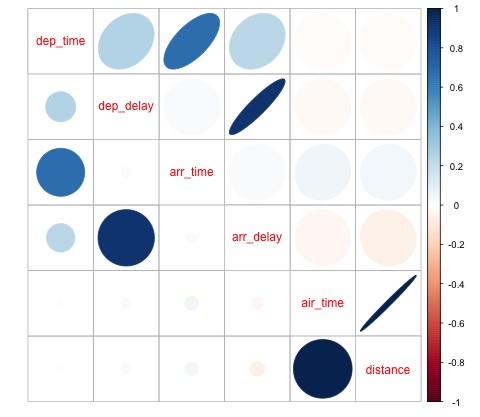
我們可以從圖中看到,資料集中的某些變數之間存在很強的相關性。例如,到達延誤和出發延誤似乎高度相關。我們可以看到這一點,因為橢圓顯示這兩個變數之間幾乎呈線性關係,但是,從這個結果中找到因果關係並不簡單。
我們不能說,因為兩個變數是相關的,所以一個變數會影響另一個變數。我們還在圖中發現飛行時間和距離之間存在很強的相關性,這在預期中是相當合理的,因為距離越遠,飛行時間應該越長。
我們還可以對資料進行單變數分析。視覺化分佈的一種簡單有效的方法是**箱線圖**。以下程式碼演示瞭如何使用ggplot2庫生成箱線圖和格子圖。此程式碼也可在**bda/part1/data_visualization/boxplots.R**檔案中找到。
source('data_visualization.R')
### Analyzing Distributions using box-plots
# The following shows the distance as a function of the carrier
p = ggplot(DT, aes(x = carrier, y = distance, fill = carrier)) + # Define the carrier
in the x axis and distance in the y axis
geom_box-plot() + # Use the box-plot geom
theme_bw() + # Leave a white background - More in line with tufte's
principles than the default
guides(fill = FALSE) + # Remove legend
labs(list(title = 'Distance as a function of carrier', # Add labels
x = 'Carrier', y = 'Distance'))
p
# Save to disk
png(‘boxplot_carrier.png’)
print(p)
dev.off()
# Let's add now another variable, the month of each flight
# We will be using facet_wrap for this
p = ggplot(DT, aes(carrier, distance, fill = carrier)) +
geom_box-plot() +
theme_bw() +
guides(fill = FALSE) +
facet_wrap(~month) + # This creates the trellis plot with the by month variable
labs(list(title = 'Distance as a function of carrier by month',
x = 'Carrier', y = 'Distance'))
p
# The plot shows there aren't clear differences between distance in different months
# Save to disk
png('boxplot_carrier_by_month.png')
print(p)
dev.off()
大資料分析 - R語言入門
本節旨在向用戶介紹R程式語言。R可以從cran網站下載。對於Windows使用者,安裝rtools和rstudio IDE很有用。
**R**背後的總體概念是充當用編譯語言(如C、C++和Fortran)開發的其他軟體的介面,併為使用者提供一個互動式工具來分析資料。
導航到書籍壓縮檔案bda/part2/R_introduction的資料夾,並開啟R_introduction.Rproj檔案。這將開啟一個RStudio會話。然後開啟01_vectors.R檔案。逐行執行指令碼並遵循程式碼中的註釋。另一個有用的學習方法是直接鍵入程式碼,這將幫助你熟悉R語法。在R中,註釋用#符號編寫。
為了顯示本書中執行R程式碼的結果,在程式碼評估後,R返回的結果將被註釋。這樣,你就可以複製貼上書中的程式碼,並在R中直接嘗試其中的部分程式碼。
# Create a vector of numbers
numbers = c(1, 2, 3, 4, 5)
print(numbers)
# [1] 1 2 3 4 5
# Create a vector of letters
ltrs = c('a', 'b', 'c', 'd', 'e')
# [1] "a" "b" "c" "d" "e"
# Concatenate both
mixed_vec = c(numbers, ltrs)
print(mixed_vec)
# [1] "1" "2" "3" "4" "5" "a" "b" "c" "d" "e"
讓我們分析一下前面程式碼中發生的情況。我們可以看到,可以用數字和字母建立向量。我們不需要事先告訴R我們想要哪種資料型別。最後,我們能夠建立一個包含數字和字母的向量。向量mixed_vec已將數字強制轉換為字元,我們可以透過檢視值如何在引號內列印來看到這一點。
下面的程式碼顯示了由class函式返回的不同向量的型別。通常使用class函式來“詢問”物件,詢問它的類是什麼。
### Evaluate the data types using class ### One dimensional objects # Integer vector num = 1:10 class(num) # [1] "integer" # Numeric vector, it has a float, 10.5 num = c(1:10, 10.5) class(num) # [1] "numeric" # Character vector ltrs = letters[1:10] class(ltrs) # [1] "character" # Factor vector fac = as.factor(ltrs) class(fac) # [1] "factor"
R也支援二維物件。在下面的程式碼中,有一些在R中最常用的兩種資料結構的示例:矩陣和data.frame。
# Matrix M = matrix(1:12, ncol = 4) # [,1] [,2] [,3] [,4] # [1,] 1 4 7 10 # [2,] 2 5 8 11 # [3,] 3 6 9 12 lM = matrix(letters[1:12], ncol = 4) # [,1] [,2] [,3] [,4] # [1,] "a" "d" "g" "j" # [2,] "b" "e" "h" "k" # [3,] "c" "f" "i" "l" # Coerces the numbers to character # cbind concatenates two matrices (or vectors) in one matrix cbind(M, lM) # [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] # [1,] "1" "4" "7" "10" "a" "d" "g" "j" # [2,] "2" "5" "8" "11" "b" "e" "h" "k" # [3,] "3" "6" "9" "12" "c" "f" "i" "l" class(M) # [1] "matrix" class(lM) # [1] "matrix" # data.frame # One of the main objects of R, handles different data types in the same object. # It is possible to have numeric, character and factor vectors in the same data.frame df = data.frame(n = 1:5, l = letters[1:5]) df # n l # 1 1 a # 2 2 b # 3 3 c # 4 4 d # 5 5 e
如前面的示例所示,可以在同一個物件中使用不同的資料型別。通常情況下,資料就是這樣在資料庫、API中呈現的,部分資料是文字或字元向量,其他是數值型。分析師的工作是確定要分配哪種統計資料型別,然後為其使用正確的R資料型別。在統計學中,我們通常認為變數具有以下型別:
- 數值型
- 名義型或分型別
- 有序型
在R中,向量可以具有以下類別:
- 數值型 - 整數型
- 因子型
- 有序因子型
R為每種統計型別的變數提供了一種資料型別。然而,有序因子很少使用,但可以透過函式factor或ordered建立。
下一節討論索引的概念。這是一個相當常見的操作,它處理選擇物件的部分並對其進行轉換的問題。
# Let's create a data.frame
df = data.frame(numbers = 1:26, letters)
head(df)
# numbers letters
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 e
# 6 6 f
# str gives the structure of a data.frame, it’s a good summary to inspect an object
str(df)
# 'data.frame': 26 obs. of 2 variables:
# $ numbers: int 1 2 3 4 5 6 7 8 9 10 ...
# $ letters: Factor w/ 26 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 9 10 ...
# The latter shows the letters character vector was coerced as a factor.
# This can be explained by the stringsAsFactors = TRUE argumnet in data.frame
# read ?data.frame for more information
class(df)
# [1] "data.frame"
### Indexing
# Get the first row
df[1, ]
# numbers letters
# 1 1 a
# Used for programming normally - returns the output as a list
df[1, , drop = TRUE]
# $numbers
# [1] 1
#
# $letters
# [1] a
# Levels: a b c d e f g h i j k l m n o p q r s t u v w x y z
# Get several rows of the data.frame
df[5:7, ]
# numbers letters
# 5 5 e
# 6 6 f
# 7 7 g
### Add one column that mixes the numeric column with the factor column
df$mixed = paste(df$numbers, df$letters, sep = ’’)
str(df)
# 'data.frame': 26 obs. of 3 variables:
# $ numbers: int 1 2 3 4 5 6 7 8 9 10 ...
# $ letters: Factor w/ 26 levels "a","b","c","d",..: 1 2 3 4 5 6 7 8 9 10 ...
# $ mixed : chr "1a" "2b" "3c" "4d" ...
### Get columns
# Get the first column
df[, 1]
# It returns a one dimensional vector with that column
# Get two columns
df2 = df[, 1:2]
head(df2)
# numbers letters
# 1 1 a
# 2 2 b
# 3 3 c
# 4 4 d
# 5 5 e
# 6 6 f
# Get the first and third columns
df3 = df[, c(1, 3)]
df3[1:3, ]
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
### Index columns from their names
names(df)
# [1] "numbers" "letters" "mixed"
# This is the best practice in programming, as many times indeces change, but
variable names don’t
# We create a variable with the names we want to subset
keep_vars = c("numbers", "mixed")
df4 = df[, keep_vars]
head(df4)
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# 6 6 6f
### subset rows and columns
# Keep the first five rows
df5 = df[1:5, keep_vars]
df5
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# subset rows using a logical condition
df6 = df[df$numbers < 10, keep_vars]
df6
# numbers mixed
# 1 1 1a
# 2 2 2b
# 3 3 3c
# 4 4 4d
# 5 5 5e
# 6 6 6f
# 7 7 7g
# 8 8 8h
# 9 9 9i
大資料分析 - SQL入門
SQL代表結構化查詢語言。它是從傳統資料倉庫和大資料技術中的資料庫中提取資料的最廣泛使用的語言之一。為了演示SQL的基礎知識,我們將使用示例。為了專注於語言本身,我們將在R內部使用SQL。在編寫SQL程式碼方面,這與在資料庫中進行的操作完全一樣。
SQL的核心是三個語句:SELECT、FROM和WHERE。以下示例使用了SQL最常見的用例。導航到資料夾bda/part2/SQL_introduction並開啟SQL_introduction.Rproj檔案。然後開啟01_select.R指令碼。為了在R中編寫SQL程式碼,我們需要安裝sqldf包,如下面的程式碼所示。
# Install the sqldf package
install.packages('sqldf')
# load the library
library('sqldf')
library(nycflights13)
# We will be working with the fligths dataset in order to introduce SQL
# Let’s take a look at the table
str(flights)
# Classes 'tbl_d', 'tbl' and 'data.frame': 336776 obs. of 16 variables:
# $ year : int 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 ...
# $ month : int 1 1 1 1 1 1 1 1 1 1 ...
# $ day : int 1 1 1 1 1 1 1 1 1 1 ...
# $ dep_time : int 517 533 542 544 554 554 555 557 557 558 ...
# $ dep_delay: num 2 4 2 -1 -6 -4 -5 -3 -3 -2 ...
# $ arr_time : int 830 850 923 1004 812 740 913 709 838 753 ...
# $ arr_delay: num 11 20 33 -18 -25 12 19 -14 -8 8 ...
# $ carrier : chr "UA" "UA" "AA" "B6" ...
# $ tailnum : chr "N14228" "N24211" "N619AA" "N804JB" ...
# $ flight : int 1545 1714 1141 725 461 1696 507 5708 79 301 ...
# $ origin : chr "EWR" "LGA" "JFK" "JFK" ...
# $ dest : chr "IAH" "IAH" "MIA" "BQN" ...
# $ air_time : num 227 227 160 183 116 150 158 53 140 138 ...
# $ distance : num 1400 1416 1089 1576 762 ...
# $ hour : num 5 5 5 5 5 5 5 5 5 5 ...
# $ minute : num 17 33 42 44 54 54 55 57 57 58 ...
select語句用於從表中檢索列並在其上進行計算。最簡單的SELECT語句在ej1中演示。我們還可以建立新的變數,如ej2所示。
### SELECT statement
ej1 = sqldf("
SELECT
dep_time
,dep_delay
,arr_time
,carrier
,tailnum
FROM
flights
")
head(ej1)
# dep_time dep_delay arr_time carrier tailnum
# 1 517 2 830 UA N14228
# 2 533 4 850 UA N24211
# 3 542 2 923 AA N619AA
# 4 544 -1 1004 B6 N804JB
# 5 554 -6 812 DL N668DN
# 6 554 -4 740 UA N39463
# In R we can use SQL with the sqldf function. It works exactly the same as in
a database
# The data.frame (in this case flights) represents the table we are querying
and goes in the FROM statement
# We can also compute new variables in the select statement using the syntax:
# old_variables as new_variable
ej2 = sqldf("
SELECT
arr_delay - dep_delay as gain,
carrier
FROM
flights
")
ej2[1:5, ]
# gain carrier
# 1 9 UA
# 2 16 UA
# 3 31 AA
# 4 -17 B6
# 5 -19 DL
SQL最常用的功能之一是group by語句。這允許計算另一個變數的不同組的數值。開啟指令碼02_group_by.R。
### GROUP BY
# Computing the average
ej3 = sqldf("
SELECT
avg(arr_delay) as mean_arr_delay,
avg(dep_delay) as mean_dep_delay,
carrier
FROM
flights
GROUP BY
carrier
")
# mean_arr_delay mean_dep_delay carrier
# 1 7.3796692 16.725769 9E
# 2 0.3642909 8.586016 AA
# 3 -9.9308886 5.804775 AS
# 4 9.4579733 13.022522 B6
# 5 1.6443409 9.264505 DL
# 6 15.7964311 19.955390 EV
# 7 21.9207048 20.215543 F9
# 8 20.1159055 18.726075 FL
# 9 -6.9152047 4.900585 HA
# 10 10.7747334 10.552041 MQ
# 11 11.9310345 12.586207 OO
# 12 3.5580111 12.106073 UA
# 13 2.1295951 3.782418 US
# 14 1.7644644 12.869421 VX
# 15 9.6491199 17.711744 WN
# 16 15.5569853 18.996330 YV
# Other aggregations
ej4 = sqldf("
SELECT
avg(arr_delay) as mean_arr_delay,
min(dep_delay) as min_dep_delay,
max(dep_delay) as max_dep_delay,
carrier
FROM
flights
GROUP BY
carrier
")
# We can compute the minimun, mean, and maximum values of a numeric value
ej4
# mean_arr_delay min_dep_delay max_dep_delay carrier
# 1 7.3796692 -24 747 9E
# 2 0.3642909 -24 1014 AA
# 3 -9.9308886 -21 225 AS
# 4 9.4579733 -43 502 B6
# 5 1.6443409 -33 960 DL
# 6 15.7964311 -32 548 EV
# 7 21.9207048 -27 853 F9
# 8 20.1159055 -22 602 FL
# 9 -6.9152047 -16 1301 HA
# 10 10.7747334 -26 1137 MQ
# 11 11.9310345 -14 154 OO
# 12 3.5580111 -20 483 UA
# 13 2.1295951 -19 500 US
# 14 1.7644644 -20 653 VX
# 15 9.6491199 -13 471 WN
# 16 15.5569853 -16 387 YV
### We could be also interested in knowing how many observations each carrier has
ej5 = sqldf("
SELECT
carrier, count(*) as count
FROM
flights
GROUP BY
carrier
")
ej5
# carrier count
# 1 9E 18460
# 2 AA 32729
# 3 AS 714
# 4 B6 54635
# 5 DL 48110
# 6 EV 54173
# 7 F9 685
# 8 FL 3260
# 9 HA 342
# 10 MQ 26397
# 11 OO 32
# 12 UA 58665
# 13 US 20536
# 14 VX 5162
# 15 WN 12275
# 16 YV 601
SQL最有用的功能是連線。連線意味著我們想要使用一列來匹配兩個表的數值,將表A和表B組合成一個表。連線有不同的型別,實際上,為了入門,這些將是最有用的:內部連線和左外部連線。
# Let’s create two tables: A and B to demonstrate joins.
A = data.frame(c1 = 1:4, c2 = letters[1:4])
B = data.frame(c1 = c(2,4,5,6), c2 = letters[c(2:5)])
A
# c1 c2
# 1 a
# 2 b
# 3 c
# 4 d
B
# c1 c2
# 2 b
# 4 c
# 5 d
# 6 e
### INNER JOIN
# This means to match the observations of the column we would join the tables by.
inner = sqldf("
SELECT
A.c1, B.c2
FROM
A INNER JOIN B
ON A.c1 = B.c1
")
# Only the rows that match c1 in both A and B are returned
inner
# c1 c2
# 2 b
# 4 c
### LEFT OUTER JOIN
# the left outer join, sometimes just called left join will return the
# first all the values of the column used from the A table
left = sqldf("
SELECT
A.c1, B.c2
FROM
A LEFT OUTER JOIN B
ON A.c1 = B.c1
")
# Only the rows that match c1 in both A and B are returned
left
# c1 c2
# 1 <NA>
# 2 b
# 3 <NA>
# 4 c
大資料分析 - 圖表
分析資料的首要方法是直觀地分析它。這樣做的目標通常是找到變數之間的關係和變數的單變數描述。我們可以將這些策略分為:
- 單變數分析
- 多變數分析
單變數圖形方法
單變數是一個統計術語。實際上,這意味著我們想要獨立於其餘資料分析一個變數。能夠有效地做到這一點的圖是:
箱線圖
箱線圖通常用於比較分佈。這是直觀檢查不同分佈之間是否存在差異的好方法。我們可以看看不同切割方式下鑽石價格是否存在差異。
# We will be using the ggplot2 library for plotting
library(ggplot2)
data("diamonds")
# We will be using the diamonds dataset to analyze distributions of numeric variables
head(diamonds)
# carat cut color clarity depth table price x y z
# 1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
# 2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
# 3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
# 4 0.29 Premium I VS2 62.4 58 334 4.20 4.23 2.63
# 5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
# 6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
### Box-Plots
p = ggplot(diamonds, aes(x = cut, y = price, fill = cut)) +
geom_box-plot() +
theme_bw()
print(p)
我們可以看到,在圖中,不同切割型別的鑽石價格分佈存在差異。
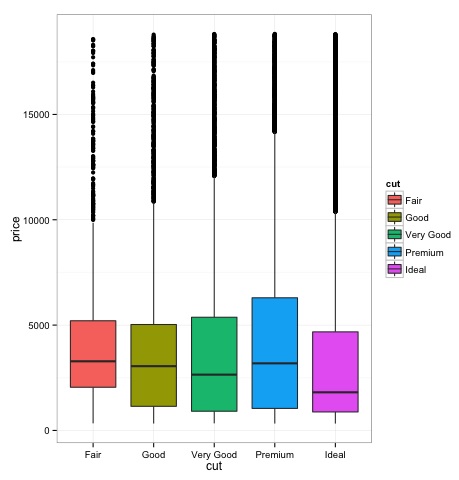
直方圖
source('01_box_plots.R')
# We can plot histograms for each level of the cut factor variable using
facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ .) +
theme_bw()
p
# the previous plot doesn’t allow to visuallize correctly the data because of
the differences in scale
# we can turn this off using the scales argument of facet_grid
p = ggplot(diamonds, aes(x = price, fill = cut)) +
geom_histogram() +
facet_grid(cut ~ ., scales = 'free') +
theme_bw()
p
png('02_histogram_diamonds_cut.png')
print(p)
dev.off()
上述程式碼的輸出如下:
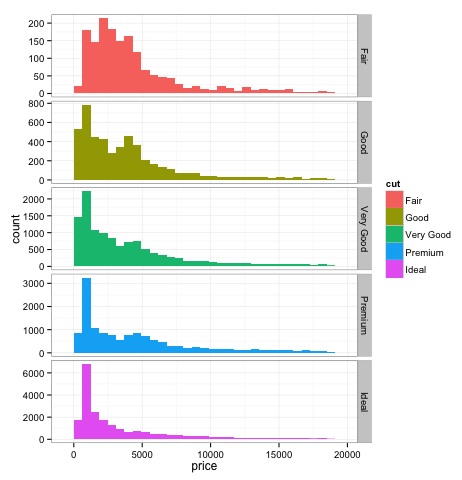
多變數圖形方法
探索性資料分析中的多變數圖形方法的目標是尋找不同變數之間的關係。通常有兩種方法可以做到這一點:繪製數值變數的相關矩陣或簡單地將原始資料繪製為散點圖矩陣。
為了演示這一點,我們將使用diamonds資料集。要遵循程式碼,請開啟指令碼bda/part2/charts/03_multivariate_analysis.R。
library(ggplot2)
data(diamonds)
# Correlation matrix plots
keep_vars = c('carat', 'depth', 'price', 'table')
df = diamonds[, keep_vars]
# compute the correlation matrix
M_cor = cor(df)
# carat depth price table
# carat 1.00000000 0.02822431 0.9215913 0.1816175
# depth 0.02822431 1.00000000 -0.0106474 -0.2957785
# price 0.92159130 -0.01064740 1.0000000 0.1271339
# table 0.18161755 -0.29577852 0.1271339 1.0000000
# plots
heat-map(M_cor)
程式碼將產生以下輸出:
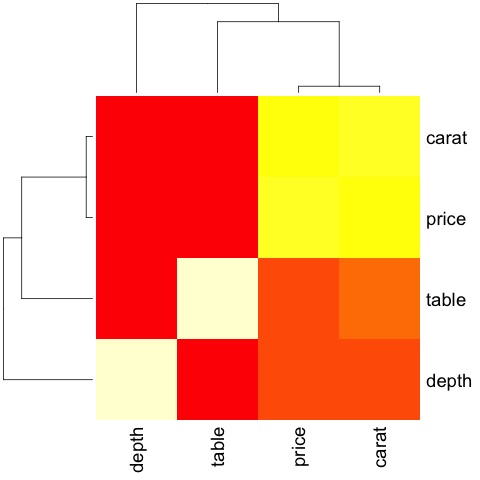
這是一個摘要,它告訴我們價格和克拉之間存在很強的相關性,而其他變數之間則沒有太多相關性。
當我們有很多變數時,相關矩陣很有用,在這種情況下,繪製原始資料是不切實際的。如前所述,也可以顯示原始資料:
library(GGally) ggpairs(df)
我們可以看到,在熱力圖中顯示的結果得到了證實,價格和克拉變數之間存在0.922的相關性。
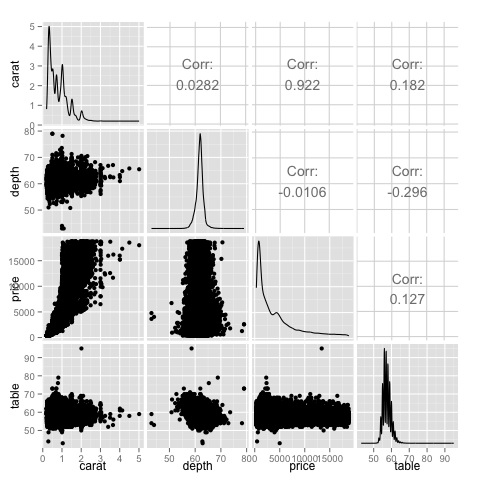
可以在散點圖矩陣的(3, 1)索引中找到的價格-克拉散點圖中直觀地看到這種關係。
大資料分析 - 資料分析工具
各種工具允許資料科學家有效地分析資料。通常,資料分析的工程方面側重於資料庫,資料科學家則側重於可以實現資料產品的工具。下一節將討論不同工具的優勢,重點是資料科學家在實踐中最常用的統計軟體包。
R程式語言
R是一種開源程式語言,專注於統計分析。就統計能力而言,它與SAS、SPSS等商業工具具有競爭力。它被認為是其他程式語言(如C、C++或Fortran)的介面。
R的另一個優勢是大量的開源庫。在CRAN中,有6000多個可以免費下載的包,在Github中,有各種各樣的R包可用。
在效能方面,R對於密集型操作來說速度很慢,鑑於大量的庫可用,程式碼的慢速部分是用編譯語言編寫的。但是,如果你打算進行需要編寫深度for迴圈的操作,那麼R就不是你的最佳選擇。對於資料分析目的,有一些很好的庫,例如data.table, glmnet, ranger, xgboost, ggplot2, caret,它們允許將R用作更快速程式語言的介面。
用於資料分析的Python
Python是一種通用程式語言,它包含大量用於資料分析的庫,例如pandas, scikit-learn, theano, numpy和scipy。
R中提供的大多數功能也可以在Python中完成,但我們發現R更易於使用。如果你正在處理大型資料集,通常Python比R更好。Python可以非常有效地逐行清理和處理資料。R也可以做到這一點,但對於指令碼任務來說,它不如Python高效。
對於機器學習,scikit-learn是一個不錯的環境,它提供了大量可以輕鬆處理中等大小資料集的演算法。與R的等效庫(caret)相比,scikit-learn具有更清晰、更一致的API。
Julia
Julia是一種用於技術計算的高階、高效能動態程式語言。它的語法與R或Python非常相似,因此,如果你已經在使用R或Python,那麼用Julia編寫相同的程式碼應該非常簡單。這門語言相當新,並且在過去幾年裡發展迅速,所以它絕對是一個不錯的選擇。
我們建議將Julia用於原型設計計算密集型演算法,例如神經網路。它是進行研究的一個好工具。在生產中實現模型方面,Python可能會有更好的選擇。然而,隨著提供R、Python和Julia模型實現工程的網路服務的出現,這個問題正變得越來越不重要。
SAS
SAS是一種商業語言,仍在用於商業智慧。它有一個基礎語言,允許使用者程式設計各種各樣的應用程式。它包含相當多的商業產品,使非專業使用者能夠使用複雜工具,例如神經網路庫,而無需程式設計。
除了商業工具的明顯缺點之外,SAS無法很好地擴充套件到大型資料集。即使是中等大小的資料集也會讓SAS出現問題,並導致伺服器崩潰。只有當你處理小型資料集並且使用者不是專業資料科學家時,才推薦使用SAS。對於高階使用者來說,R和Python提供了更高效的環境。
SPSS
SPSS是IBM目前用於統計分析的產品。它主要用於分析調查資料,對於無法程式設計的使用者來說,它是一個不錯的選擇。它可能與SAS一樣易於使用,但在實現模型方面,它更簡單,因為它提供SQL程式碼來評分模型。這段程式碼通常效率不高,但這是一個開始,而SAS則分別為每個資料庫銷售評分模型的產品。對於小型資料和缺乏經驗的團隊,SPSS是一個與SAS一樣好的選擇。
然而,該軟體的功能相當有限,經驗豐富的使用者使用R或Python的效率要高得多。
Matlab,Octave
還有一些其他可用的工具,例如Matlab或其開源版本(Octave)。這些工具主要用於研究。就功能而言,R或Python可以實現Matlab或Octave的所有功能。只有當您對它們提供的支援感興趣時,購買產品的許可證才有意義。
大資料分析 - 統計方法
在分析資料時,可以使用統計方法。執行基本分析所需的工具包括:
- 相關性分析
- 方差分析
- 假設檢驗
處理大型資料集時,這不會造成問題,因為這些方法在計算上並不密集,相關性分析除外。在這種情況下,始終可以抽取樣本,結果應該是穩健的。
相關性分析
相關性分析旨在尋找數值變數之間的線性關係。這在不同的情況下都很有用。一個常見的用途是探索性資料分析,書中16.0.2節有一個這種方法的基本示例。首先,上述示例中使用的相關性度量基於**皮爾遜係數**。然而,還有一個有趣的相關性度量不受異常值的影響。這個度量稱為斯皮爾曼相關性。
**斯皮爾曼相關性**度量比皮爾遜方法更能抵抗異常值的影響,並且在資料不服從正態分佈時,能夠更好地估計數值變數之間的線性關係。
library(ggplot2)
# Select variables that are interesting to compare pearson and spearman
correlation methods.
x = diamonds[, c('x', 'y', 'z', 'price')]
# From the histograms we can expect differences in the correlations of both
metrics.
# In this case as the variables are clearly not normally distributed, the
spearman correlation
# is a better estimate of the linear relation among numeric variables.
par(mfrow = c(2,2))
colnm = names(x)
for(i in 1:4) {
hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i]))
}
par(mfrow = c(1,1))
從下圖中的直方圖可以看出,兩種度量的相關性存在差異。在這種情況下,由於變數顯然不服從正態分佈,因此斯皮爾曼相關性是數值變數之間線性關係的更好估計。
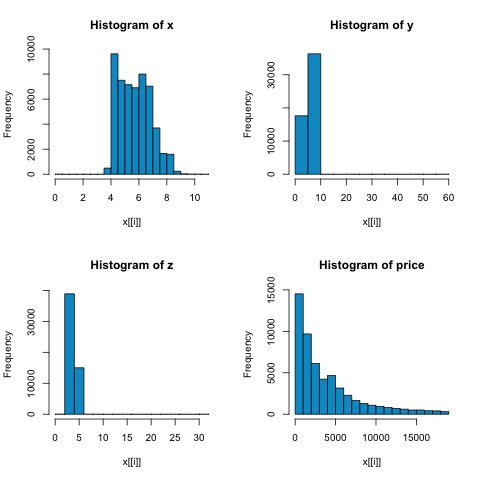
要在R中計算相關性,請開啟包含此程式碼段的檔案**bda/part2/statistical_methods/correlation/correlation.R**。
## Correlation Matrix - Pearson and spearman cor_pearson <- cor(x, method = 'pearson') cor_spearman <- cor(x, method = 'spearman') ### Pearson Correlation print(cor_pearson) # x y z price # x 1.0000000 0.9747015 0.9707718 0.8844352 # y 0.9747015 1.0000000 0.9520057 0.8654209 # z 0.9707718 0.9520057 1.0000000 0.8612494 # price 0.8844352 0.8654209 0.8612494 1.0000000 ### Spearman Correlation print(cor_spearman) # x y z price # x 1.0000000 0.9978949 0.9873553 0.9631961 # y 0.9978949 1.0000000 0.9870675 0.9627188 # z 0.9873553 0.9870675 1.0000000 0.9572323 # price 0.9631961 0.9627188 0.9572323 1.0000000
卡方檢驗
卡方檢驗允許我們檢驗兩個隨機變數是否獨立。這意味著每個變數的機率分佈不會影響另一個變數。為了在R中評估該檢驗,我們首先需要建立一個列聯表,然後將該表傳遞給**chisq.test R**函式。
例如,讓我們檢查diamonds資料集中的cut和color變數之間是否存在關聯。該檢驗正式定義如下:
- H0:變數cut和color是獨立的
- H1:變數cut和color不是獨立的
從變數名稱來看,我們假設這兩個變數之間存在關係,但是該檢驗可以提供一個客觀的“規則”,說明該結果的顯著性如何。
在下面的程式碼片段中,我們發現該檢驗的p值為2.2e-16,這在實踐中幾乎為零。然後在進行**蒙特卡羅模擬**後執行該檢驗,我們發現p值為0.0004998,這仍然遠低於閾值0.05。此結果意味著我們拒絕零假設(H0),因此我們認為變數**cut**和**color**不是獨立的。
library(ggplot2) # Use the table function to compute the contingency table tbl = table(diamonds$cut, diamonds$color) tbl # D E F G H I J # Fair 163 224 312 314 303 175 119 # Good 662 933 909 871 702 522 307 # Very Good 1513 2400 2164 2299 1824 1204 678 # Premium 1603 2337 2331 2924 2360 1428 808 # Ideal 2834 3903 3826 4884 3115 2093 896 # In order to run the test we just use the chisq.test function. chisq.test(tbl) # Pearson’s Chi-squared test # data: tbl # X-squared = 310.32, df = 24, p-value < 2.2e-16 # It is also possible to compute the p-values using a monte-carlo simulation # It's needed to add the simulate.p.value = TRUE flag and the amount of simulations chisq.test(tbl, simulate.p.value = TRUE, B = 2000) # Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates) # data: tbl # X-squared = 310.32, df = NA, p-value = 0.0004998
t檢驗
**t檢驗**的目的是評估名義變數的不同組之間數值變數的分佈是否存在差異。為了證明這一點,我將選擇因子變數cut的Fair和Ideal水平,然後我們將比較這兩個組中數值變數的值。
data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]
data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the
cut variable
df1 = data[, c('cut', 'price')]
# We can see the price means are different for each group
tapply(df1$price, df1$cut, mean)
# Fair Ideal
# 4358.758 3457.542
t檢驗在R中使用**t.test**函式實現。t.test的公式介面是最簡單的使用方法,其思想是用一個組變數來解釋一個數值變數。
例如:**t.test(numeric_variable ~ group_variable, data = data)**。在前面的示例中,**numeric_variable**是**price**,**group_variable**是**cut**。
從統計學的角度來看,我們正在檢驗數值變數在兩組之間的分佈是否存在差異。正式的假設檢驗是用零假設(H0)和備擇假設(H1)來描述的。
H0:Fair和Ideal組之間價格變數的分佈沒有差異
H1:Fair和Ideal組之間價格變數的分佈存在差異
以下可以在R中使用以下程式碼實現:
t.test(price ~ cut, data = data) # Welch Two Sample t-test # # data: price by cut # t = 9.7484, df = 1894.8, p-value < 2.2e-16 # alternative hypothesis: true difference in means is not equal to 0 # 95 percent confidence interval: # 719.9065 1082.5251 # sample estimates: # mean in group Fair mean in group Ideal # 4358.758 3457.542 # Another way to validate the previous results is to just plot the distributions using a box-plot plot(price ~ cut, data = data, ylim = c(0,12000), col = 'deepskyblue3')
我們可以透過檢查p值是否低於0.05來分析檢驗結果。如果是這種情況,我們將保留備擇假設。這意味著我們在cut因子的兩個水平之間發現了價格差異。從水平名稱來看,我們本應該預料到這個結果,但是我們沒有預料到Fail組的平均價格會高於Ideal組。我們可以透過比較每個因子的均值來觀察這一點。
**plot**命令生成一個圖形,顯示價格和cut變數之間的關係。這是一個箱線圖;我們在16.0.1節中介紹過這種圖,但它基本上顯示了我們正在分析的cut的兩個水平的價格變數的分佈。
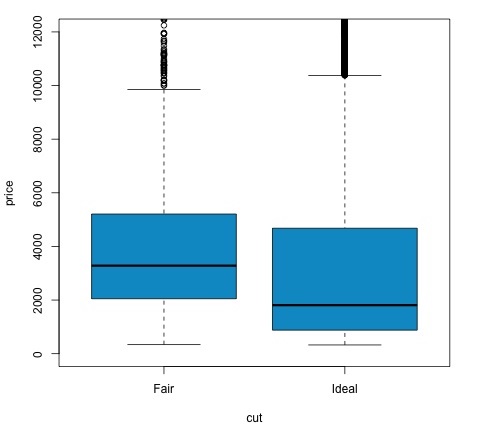
方差分析
方差分析(ANOVA)是一種統計模型,用於透過比較每個組的均值和方差來分析組分佈之間的差異,該模型由羅納德·費舍爾開發。ANOVA提供了一個統計檢驗,用於檢驗多個組的均值是否相等,因此它將t檢驗推廣到兩個以上組。
ANOVA對於比較三個或更多組的統計顯著性非常有用,因為進行多個雙樣本t檢驗會導致犯I類統計錯誤的可能性增加。
就提供數學解釋而言,需要理解以下內容才能理解該檢驗。
xij = x + (xi − x) + (xij − x)
這導致以下模型:
xij = μ + αi + ∈ij
其中μ是總均值,αi是第i個組的均值。誤差項∈ij假定是從正態分佈中獨立同分布的。該檢驗的零假設是:
α1 = α2 = … = αk
就計算檢驗統計量而言,我們需要計算兩個值:
- 組間差異的平方和:
$$SSD_B = \sum_{i}^{k} \sum_{j}^{n}(\bar{x_{\bar{i}}} - \bar{x})^2$$
- 組內平方和
$$SSD_W = \sum_{i}^{k} \sum_{j}^{n}(\bar{x_{\bar{ij}}} - \bar{x_{\bar{i}}})^2$$
其中SSDB的自由度為k−1,SSDW的自由度為N−k。然後我們可以定義每個度量的均方差。
MSB = SSDB / (k - 1)
MSw = SSDw / (N - k)
最後,ANOVA中的檢驗統計量定義為上述兩個量的比率
F = MSB / MSw
它服從自由度為k−1和N−k的F分佈。如果零假設為真,F值可能接近1。否則,組間均方MSB可能較大,導致F值較大。
基本上,ANOVA檢查總方差的兩個來源,並檢視哪個部分貢獻更大。這就是為什麼它被稱為方差分析,儘管目的是比較組均值。
就計算統計量而言,在R中實際上相當簡單。以下示例將演示如何執行此操作以及如何繪製結果。
library(ggplot2)
# We will be using the mtcars dataset
head(mtcars)
# mpg cyl disp hp drat wt qsec vs am gear carb
# Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
# Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
# Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
# Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
# Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
# Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
# Let's see if there are differences between the groups of cyl in the mpg variable.
data = mtcars[, c('mpg', 'cyl')]
fit = lm(mpg ~ cyl, data = mtcars)
anova(fit)
# Analysis of Variance Table
# Response: mpg
# Df Sum Sq Mean Sq F value Pr(>F)
# cyl 1 817.71 817.71 79.561 6.113e-10 ***
# Residuals 30 308.33 10.28
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .
# Plot the distribution
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')
程式碼將產生以下輸出:
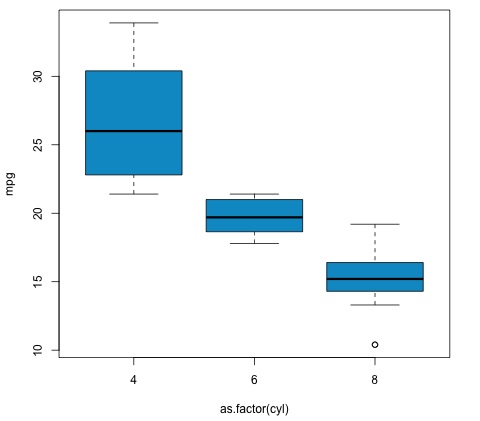
我們在示例中獲得的p值明顯小於0.05,因此R返回符號'***'來表示這一點。這意味著我們拒絕零假設,並且我們在cyl變數的不同組之間發現了mpg均值的差異。
機器學習用於資料分析
機器學習是計算機科學的一個子領域,它處理模式識別、計算機視覺、語音識別、文字分析等任務,並且與統計學和數學最佳化有著密切的聯絡。應用包括搜尋引擎的開發、垃圾郵件過濾、光學字元識別(OCR)等。資料探勘、模式識別和統計學習領域之間的界限並不清晰,基本上都指類似的問題。
機器學習可以分為兩種型別的任務:
- 監督學習
- 無監督學習
監督學習
監督學習指的是一種問題型別,其中輸入資料定義為矩陣X,我們感興趣的是預測響應y。其中X = {x1, x2, …, xn}具有n個預測變數,並且具有兩個值y = {c1, c2}。
一個示例應用程式是使用人口統計特徵作為預測變數來預測網頁使用者點選廣告的機率。這通常被稱為預測點選率(CTR)。然後y = {點選,不點選},預測變數可以是使用的IP地址、使用者進入網站的日期、使用者的城市、國家以及其他可能可用的特徵。
無監督學習
無監督學習處理在沒有要學習的類別的情況下查詢彼此相似的組的問題。有多種方法可以將預測變數對映到查詢在每個組中共享相似例項並在彼此之間不同的組。
無監督學習的一個示例應用程式是客戶細分。例如,在電信行業中,一個常見的任務是根據使用者對電話的使用情況對使用者進行細分。這將允許營銷部門針對每個組使用不同的產品。
大資料分析 - 樸素貝葉斯分類器
樸素貝葉斯是一種用於構建分類器的機率技術。樸素貝葉斯分類器的特徵假設是認為,給定類別變數,特定特徵的值獨立於任何其他特徵的值。
儘管前面提到了過於簡化的假設,但樸素貝葉斯分類器在複雜的現實世界情況中具有良好的結果。樸素貝葉斯的優點是它只需要少量訓練資料來估計分類所需的必要引數,並且可以增量地訓練分類器。
樸素貝葉斯是一個條件機率模型:給定一個要分類的問題例項,該例項由表示一些n個特徵(自變數)的向量x = (x1, …, xn)表示,它為每個K個可能的輸出或類別分配此例項的機率。
$$p(C_k|x_1,....., x_n)$$
上述公式的問題在於,如果特徵數量 n 很大,或者某個特徵可以取很多值,那麼基於機率表構建這樣的模型是不可行的。因此,我們重新構建模型使其更簡單。利用貝葉斯定理,條件機率可以分解為:
$$p(C_k|x) = \frac{p(C_k)p(x|C_k)}{p(x)}$$
這意味著在上述獨立性假設下,類變數 C 的條件分佈為:
$$p(C_k|x_1,....., x_n)\: = \: \frac{1}{Z}p(C_k)\prod_{i = 1}^{n}p(x_i|C_k)$$
其中證據 Z = p(x) 是一個僅依賴於 x1, …, xn 的比例因子,如果特徵變數的值已知,則為常數。一個常見的規則是選擇最可能的假設;這被稱為最大後驗機率或 MAP 決策規則。相應的分類器,即貝葉斯分類器,是一個函式,它如下分配類標籤 $\hat{y} = C_k$ (其中 k 為某值):
$$\hat{y} = argmax\: p(C_k)\prod_{i = 1}^{n}p(x_i|C_k)$$
在 R 中實現該演算法是一個簡單的過程。以下示例演示瞭如何訓練樸素貝葉斯分類器並將其用於垃圾郵件過濾問題中的預測。
以下指令碼位於 bda/part3/naive_bayes/naive_bayes.R 檔案中。
# Install these packages
pkgs = c("klaR", "caret", "ElemStatLearn")
install.packages(pkgs)
library('ElemStatLearn')
library("klaR")
library("caret")
# Split the data in training and testing
inx = sample(nrow(spam), round(nrow(spam) * 0.9))
train = spam[inx,]
test = spam[-inx,]
# Define a matrix with features, X_train
# And a vector with class labels, y_train
X_train = train[,-58]
y_train = train$spam
X_test = test[,-58]
y_test = test$spam
# Train the model
nb_model = train(X_train, y_train, method = 'nb',
trControl = trainControl(method = 'cv', number = 3))
# Compute
preds = predict(nb_model$finalModel, X_test)$class
tbl = table(y_test, yhat = preds)
sum(diag(tbl)) / sum(tbl)
# 0.7217391
從結果可以看出,樸素貝葉斯模型的準確率為 72%。這意味著該模型正確分類了 72% 的例項。
大資料分析 - K 均值聚類
K 均值聚類旨在將 n 個觀測值劃分為 k 個簇,其中每個觀測值都屬於具有最近均值的簇,該均值作為簇的原型。這導致資料空間被劃分為 Voronoi 單元。
給定一組觀測值 (x1, x2, …, xn),其中每個觀測值都是一個 d 維實數向量,K 均值聚類旨在將 n 個觀測值劃分為 k 個組 G = {G1, G2, …, Gk},以最小化如下定義的簇內平方和 (WCSS):
$$argmin \: \sum_{i = 1}^{k} \sum_{x \in S_{i}}\parallel x - \mu_{i}\parallel ^2$$
後面的公式顯示了為了找到 K 均值聚類中的最佳原型而最小化的目標函式。該公式的直覺是,我們希望找到彼此不同的組,並且每個組的每個成員都應該與該簇的其他成員相似。
以下示例演示瞭如何在 R 中執行 K 均值聚類演算法。
library(ggplot2)
# Prepare Data
data = mtcars
# We need to scale the data to have zero mean and unit variance
data <- scale(data)
# Determine number of clusters
wss <- (nrow(data)-1)*sum(apply(data,2,var))
for (i in 2:dim(data)[2]) {
wss[i] <- sum(kmeans(data, centers = i)$withinss)
}
# Plot the clusters
plot(1:dim(data)[2], wss, type = "b", xlab = "Number of Clusters",
ylab = "Within groups sum of squares")
為了找到 K 的一個好值,我們可以繪製不同 K 值的組內平方和。此度量通常隨著新增更多組而減少,我們希望找到組內平方和的減少開始緩慢減少的點。在圖中,此值最好由 K = 6 表示。
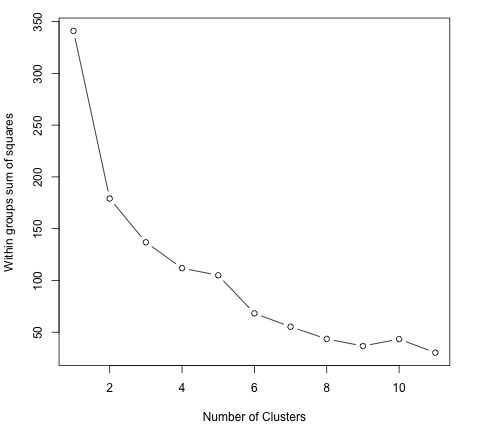
現在 K 值已定義,需要使用該值執行演算法。
# K-Means Cluster Analysis fit <- kmeans(data, 5) # 5 cluster solution # get cluster means aggregate(data,by = list(fit$cluster),FUN = mean) # append cluster assignment data <- data.frame(data, fit$cluster)
大資料分析 - 關聯規則
設 I = i1, i2, ..., in 為一組 n 個二元屬性,稱為專案。設 D = t1, t2, ..., tm 為一組事務,稱為資料庫。D 中的每個事務都有一個唯一的事務 ID,幷包含 I 中專案的子集。規則定義為 X ⇒ Y 形式的蘊涵,其中 X, Y ⊆ I 且 X ∩ Y = ∅。
專案集(簡稱專案集)X 和 Y 分別稱為規則的前件(左側或 LHS)和後件(右側或 RHS)。
為了說明這些概念,我們使用超市領域的一個小例子。專案集為 I = {牛奶、麵包、黃油、啤酒},包含這些專案的小型資料庫如下表所示。
| 事務 ID | 專案 |
|---|---|
| 1 | 牛奶、麵包 |
| 2 | 麵包、黃油 |
| 3 | 啤酒 |
| 4 | 牛奶、麵包、黃油 |
| 5 | 麵包、黃油 |
超市的一個示例規則可能是 {牛奶、麵包} ⇒ {黃油},這意味著如果購買了牛奶和麵包,顧客也會購買黃油。為了從所有可能的規則集中選擇有趣的規則,可以使用對各種顯著性和興趣度量的約束。最著名的約束是支援和置信度的最小閾值。
專案集 X 的支援 supp(X) 定義為資料集中包含該專案集的事務的比例。在表 1 的示例資料庫中,專案集 {牛奶、麵包} 的支援度為 2/5 = 0.4,因為它出現在 40% 的所有事務中(5 個事務中的 2 個)。查詢頻繁專案集可以看作是無監督學習問題的簡化。
規則的置信度定義為 conf(X ⇒ Y ) = supp(X ∪ Y )/supp(X)。例如,規則 {牛奶、麵包} ⇒ {黃油} 在表 1 的資料庫中的置信度為 0.2/0.4 = 0.5,這意味著對於包含牛奶和麵包的事務的 50%,該規則是正確的。置信度可以解釋為機率 P(Y|X) 的估計值,即在這些事務也包含 LHS 的條件下,在事務中找到規則 RHS 的機率。
在位於 bda/part3/apriori.R 中的指令碼中,可以找到實現 Apriori 演算法 的程式碼。
# Load the library for doing association rules
# install.packages(’arules’)
library(arules)
# Data preprocessing
data("AdultUCI")
AdultUCI[1:2,]
AdultUCI[["fnlwgt"]] <- NULL
AdultUCI[["education-num"]] <- NULL
AdultUCI[[ "age"]] <- ordered(cut(AdultUCI[[ "age"]], c(15,25,45,65,100)),
labels = c("Young", "Middle-aged", "Senior", "Old"))
AdultUCI[[ "hours-per-week"]] <- ordered(cut(AdultUCI[[ "hours-per-week"]],
c(0,25,40,60,168)), labels = c("Part-time", "Full-time", "Over-time", "Workaholic"))
AdultUCI[[ "capital-gain"]] <- ordered(cut(AdultUCI[[ "capital-gain"]],
c(-Inf,0,median(AdultUCI[[ "capital-gain"]][AdultUCI[[ "capitalgain"]]>0]),Inf)),
labels = c("None", "Low", "High"))
AdultUCI[[ "capital-loss"]] <- ordered(cut(AdultUCI[[ "capital-loss"]],
c(-Inf,0, median(AdultUCI[[ "capital-loss"]][AdultUCI[[ "capitalloss"]]>0]),Inf)),
labels = c("none", "low", "high"))
為了使用 Apriori 演算法生成規則,我們需要建立一個事務矩陣。以下程式碼顯示瞭如何在 R 中執行此操作。
# Convert the data into a transactions format
Adult <- as(AdultUCI, "transactions")
Adult
# transactions in sparse format with
# 48842 transactions (rows) and
# 115 items (columns)
summary(Adult)
# Plot frequent item-sets
itemFrequencyPlot(Adult, support = 0.1, cex.names = 0.8)
# generate rules
min_support = 0.01
confidence = 0.6
rules <- apriori(Adult, parameter = list(support = min_support, confidence = confidence))
rules
inspect(rules[100:110, ])
# lhs rhs support confidence lift
# {occupation = Farming-fishing} => {sex = Male} 0.02856148 0.9362416 1.4005486
# {occupation = Farming-fishing} => {race = White} 0.02831579 0.9281879 1.0855456
# {occupation = Farming-fishing} => {native-country 0.02671881 0.8758389 0.9759474
= United-States}
大資料分析 - 決策樹
決策樹是一種用於監督學習問題的演算法,例如分類或迴歸。決策樹或分類樹是一棵樹,其中每個內部(非葉)節點都用輸入特徵標記。來自用特徵標記的節點的弧線用特徵的每個可能值標記。樹的每個葉子都用一個類或一個類上的機率分佈標記。
可以透過基於屬性值測試將源集拆分為子集來“學習”樹。此過程以遞迴方式重複應用於每個派生子集,稱為遞迴劃分。當節點處的子集具有目標變數的相同值,或者拆分不再增加預測的價值時,遞迴完成。這種自上而下歸納決策樹的過程是貪婪演算法的一個例子,也是學習決策樹最常見的策略。
資料探勘中使用的決策樹主要有兩種:
分類樹 - 當響應是名義變數時,例如電子郵件是否是垃圾郵件。
迴歸樹 - 當預測結果可以被認為是一個實數時(例如,工人的工資)。
決策樹是一種簡單的方法,因此存在一些問題。其中一個問題是決策樹產生的結果模型的高方差。為了減輕這個問題,開發了決策樹的整合方法。目前廣泛使用的整合方法有兩類:
Bagging 決策樹 - 透過重複地用替換方法重新取樣訓練資料,並對樹進行投票以獲得一致性預測,來構建多個決策樹。該演算法被稱為隨機森林。
Boosting 決策樹 - 梯度提升將弱學習器組合;在這種情況下,將決策樹以迭代的方式組合成一個強大的學習器。它將一個弱樹擬合到資料,並迭代地繼續擬合弱學習器以糾正先前模型的錯誤。
# Install the party package
# install.packages('party')
library(party)
library(ggplot2)
head(diamonds)
# We will predict the cut of diamonds using the features available in the
diamonds dataset.
ct = ctree(cut ~ ., data = diamonds)
# plot(ct, main="Conditional Inference Tree")
# Example output
# Response: cut
# Inputs: carat, color, clarity, depth, table, price, x, y, z
# Number of observations: 53940
#
# 1) table <= 57; criterion = 1, statistic = 10131.878
# 2) depth <= 63; criterion = 1, statistic = 8377.279
# 3) table <= 56.4; criterion = 1, statistic = 226.423
# 4) z <= 2.64; criterion = 1, statistic = 70.393
# 5) clarity <= VS1; criterion = 0.989, statistic = 10.48
# 6) color <= E; criterion = 0.997, statistic = 12.829
# 7)* weights = 82
# 6) color > E
#Table of prediction errors
table(predict(ct), diamonds$cut)
# Fair Good Very Good Premium Ideal
# Fair 1388 171 17 0 14
# Good 102 2912 499 26 27
# Very Good 54 998 3334 249 355
# Premium 44 711 5054 11915 1167
# Ideal 22 114 3178 1601 19988
# Estimated class probabilities
probs = predict(ct, newdata = diamonds, type = "prob")
probs = do.call(rbind, probs)
head(probs)
大資料分析 - 邏輯迴歸
邏輯迴歸是一種分類模型,其中響應變數是分類的。這是一種來自統計學的演算法,用於監督分類問題。在邏輯迴歸中,我們試圖找到以下等式中引數向量 β,以最小化成本函式。
$$logit(p_i) = ln \left ( \frac{p_i}{1 - p_i} \right ) = \beta_0 + \beta_1x_{1,i} + ... + \beta_kx_{k,i}$$
以下程式碼演示瞭如何在 R 中擬合邏輯迴歸模型。我們將在這裡使用與樸素貝葉斯相同的垃圾郵件資料集來演示邏輯迴歸。
從準確性方面的預測結果來看,我們發現迴歸模型在測試集中的準確率達到了 92.5%,而樸素貝葉斯分類器的準確率為 72%。
library(ElemStatLearn) head(spam) # Split dataset in training and testing inx = sample(nrow(spam), round(nrow(spam) * 0.8)) train = spam[inx,] test = spam[-inx,] # Fit regression model fit = glm(spam ~ ., data = train, family = binomial()) summary(fit) # Call: # glm(formula = spam ~ ., family = binomial(), data = train) # # Deviance Residuals: # Min 1Q Median 3Q Max # -4.5172 -0.2039 0.0000 0.1111 5.4944 # Coefficients: # Estimate Std. Error z value Pr(>|z|) # (Intercept) -1.511e+00 1.546e-01 -9.772 < 2e-16 *** # A.1 -4.546e-01 2.560e-01 -1.776 0.075720 . # A.2 -1.630e-01 7.731e-02 -2.108 0.035043 * # A.3 1.487e-01 1.261e-01 1.179 0.238591 # A.4 2.055e+00 1.467e+00 1.401 0.161153 # A.5 6.165e-01 1.191e-01 5.177 2.25e-07 *** # A.6 7.156e-01 2.768e-01 2.585 0.009747 ** # A.7 2.606e+00 3.917e-01 6.652 2.88e-11 *** # A.8 6.750e-01 2.284e-01 2.955 0.003127 ** # A.9 1.197e+00 3.362e-01 3.559 0.000373 *** # Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 . 0.1 1 ### Make predictions preds = predict(fit, test, type = ’response’) preds = ifelse(preds > 0.5, 1, 0) tbl = table(target = test$spam, preds) tbl # preds # target 0 1 # email 535 23 # spam 46 316 sum(diag(tbl)) / sum(tbl) # 0.925
大資料分析 - 時間序列分析
時間序列是以日期或時間戳為索引的分類或數值變數的一系列觀測值。股票價格的時間序列是時間序列資料的清晰示例。在下表中,我們可以看到時間序列資料的基本結構。在這種情況下,每小時記錄一次觀測值。
| 時間戳 | 股票價格 |
|---|---|
| 2015-10-11 09:00:00 | 100 |
| 2015-10-11 10:00:00 | 110 |
| 2015-10-11 11:00:00 | 105 |
| 2015-10-11 12:00:00 | 90 |
| 2015-10-11 13:00:00 | 120 |
通常,時間序列分析的第一步是繪製序列,這通常使用折線圖完成。
時間序列分析最常見的應用是使用資料的時態結構預測數值變數的未來值。這意味著,使用可用的觀測值來預測未來的值。
資料的時態排序意味著傳統的迴歸方法沒有用。為了構建穩健的預測,我們需要考慮資料的時態排序的模型。
時間序列分析中最廣泛使用的模型稱為自迴歸移動平均 (ARMA)。該模型由兩部分組成:自迴歸 (AR) 部分和移動平均 (MA) 部分。然後,該模型通常被稱為ARMA(p, q) 模型,其中p 是自迴歸部分的階數,q 是移動平均部分的階數。
自迴歸模型
AR(p) 讀作 p 階自迴歸模型。數學上寫成:
$$X_t = c + \sum_{i = 1}^{P} \phi_i X_{t - i} + \varepsilon_{t}$$
其中 {φ1, …, φp} 是要估計的引數,c 是一個常數,隨機變數 εt 表示白噪聲。引數值需要一些約束,以便模型保持平穩。
移動平均
MA(q) 表示 q 階移動平均模型:
$$X_t = \mu + \varepsilon_t + \sum_{i = 1}^{q} \theta_i \varepsilon_{t - i}$$
其中 θ1, ..., θq 是模型的引數,μ 是 Xt 的期望值,εt, εt − 1, ... 是白噪聲誤差項。
自迴歸移動平均
ARMA(p, q) 模型結合了 p 個自迴歸項和 q 個移動平均項。數學上,該模型用以下公式表示:
$$X_t = c + \varepsilon_t + \sum_{i = 1}^{P} \phi_iX_{t - 1} + \sum_{i = 1}^{q} \theta_i \varepsilon_{t-i}$$
我們可以看到,ARMA(p, q) 模型是AR(p) 和MA(q) 模型的組合。
為了更好地理解模型,可以考慮方程中的AR部分旨在估計Xt − i觀測值的引數,以預測變數Xt的值。最終,它是一個過去值的加權平均值。MA部分採用相同的方法,但使用的是先前觀測值的誤差εt − i。因此,最終模型的結果是一個加權平均值。
下面的程式碼片段演示瞭如何在R中實現ARMA(p, q)。
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)
繪製資料通常是第一步,以找出資料中是否存在時間結構。從圖中可以看出,每年的年底都有很強的峰值。
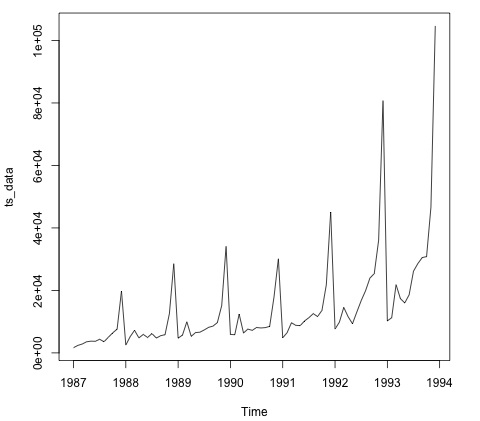
下面的程式碼將ARMA模型擬合到資料。它執行多個模型組合,並選擇誤差較小的模型。
# Fit the ARMA model fit = auto.arima(ts_data) summary(fit) # Series: ts_data # ARIMA(1,1,1)(0,1,1)[12] # Coefficients: # ar1 ma1 sma1 # 0.2401 -0.9013 0.7499 # s.e. 0.1427 0.0709 0.1790 # # sigma^2 estimated as 15464184: log likelihood = -693.69 # AIC = 1395.38 AICc = 1395.98 BIC = 1404.43 # Training set error measures: # ME RMSE MAE MPE MAPE MASE ACF1 # Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172
大資料分析 - 文字分析
在本章中,我們將使用本書第一部分中抓取的資料。資料包含描述自由職業者個人資料及其以美元計價的小時費率的文字。下一節的目的是擬合一個模型,根據自由職業者的技能,我們可以預測其每小時的工資。
下面的程式碼展示瞭如何將此案例中包含使用者技能的原始文字轉換為詞袋矩陣。為此,我們使用一個名為tm的R庫。這意味著,對於語料庫中的每個單詞,我們都會建立一個變數,其中包含每個變量出現的次數。
library(tm)
library(data.table)
source('text_analytics/text_analytics_functions.R')
data = fread('text_analytics/data/profiles.txt')
rate = as.numeric(data$rate)
keep = !is.na(rate)
rate = rate[keep]
### Make bag of words of title and body
X_all = bag_words(data$user_skills[keep])
X_all = removeSparseTerms(X_all, 0.999)
X_all
# <<DocumentTermMatrix (documents: 389, terms: 1422)>>
# Non-/sparse entries: 4057/549101
# Sparsity : 99%
# Maximal term length: 80
# Weighting : term frequency - inverse document frequency (normalized) (tf-idf)
### Make a sparse matrix with all the data
X_all <- as_sparseMatrix(X_all)
現在我們已經將文字表示為稀疏矩陣,我們可以擬合一個能夠提供稀疏解的模型。對於這種情況,一個不錯的選擇是使用LASSO(最小絕對收縮和選擇運算元)。這是一個能夠選擇最相關的特徵來預測目標的迴歸模型。
train_inx = 1:200 X_train = X_all[train_inx, ] y_train = rate[train_inx] X_test = X_all[-train_inx, ] y_test = rate[-train_inx] # Train a regression model library(glmnet) fit <- cv.glmnet(x = X_train, y = y_train, family = 'gaussian', alpha = 1, nfolds = 3, type.measure = 'mae') plot(fit) # Make predictions predictions = predict(fit, newx = X_test) predictions = as.vector(predictions[,1]) head(predictions) # 36.23598 36.43046 51.69786 26.06811 35.13185 37.66367 # We can compute the mean absolute error for the test data mean(abs(y_test - predictions)) # 15.02175
現在我們有一個模型,可以根據一組技能預測自由職業者的每小時工資。如果收集更多資料,模型的效能將會提高,但是實現此流程的程式碼將保持不變。
大資料分析 - 線上學習
線上學習是機器學習的一個子領域,它允許將監督學習模型擴充套件到海量資料集。其基本思想是,我們不需要將所有資料都讀入記憶體中才能擬合模型,只需要一次讀取每個例項。
在本例中,我們將展示如何使用邏輯迴歸實現線上學習演算法。與大多數監督學習演算法一樣,存在一個被最小化的成本函式。在邏輯迴歸中,成本函式定義為:
$$J(\theta) \: = \: \frac{-1}{m} \left [ \sum_{i = 1}^{m}y^{(i)}log(h_{\theta}(x^{(i)})) + (1 - y^{(i)}) log(1 - h_{\theta}(x^{(i)})) \right ]$$
其中J(θ)表示成本函式,hθ(x)表示假設。在邏輯迴歸的情況下,它由以下公式定義:
$$h_\theta(x) = \frac{1}{1 + e^{\theta^T x}}$$
現在我們已經定義了成本函式,我們需要找到一個演算法來最小化它。實現此目的最簡單的演算法稱為隨機梯度下降。邏輯迴歸模型權重的演算法更新規則定義為:
$$\theta_j : = \theta_j - \alpha(h_\theta(x) - y)x$$
此演算法有幾種實現方式,但是vowpal wabbit庫中的實現是迄今為止最完善的。該庫允許訓練大規模迴歸模型,並使用少量RAM。用建立者自己的話說,它被描述為:“Vowpal Wabbit (VW) 專案是一個快速的out-of-core學習系統,由微軟研究院和(以前)雅虎研究院贊助”。
我們將使用來自kaggle競賽的泰坦尼克號資料集。原始資料可以在bda/part3/vw資料夾中找到。這裡,我們有兩個檔案:
- 我們有訓練資料(train_titanic.csv),以及
- 未標記資料,以便進行新的預測(test_titanic.csv)。
為了將csv格式轉換為vowpal wabbit輸入格式,請使用csv_to_vowpal_wabbit.py python指令碼。顯然,你需要安裝python才能做到這一點。導航到bda/part3/vw資料夾,開啟終端並執行以下命令:
python csv_to_vowpal_wabbit.py
請注意,對於本節,如果您使用的是Windows,則需要安裝Unix命令列,請訪問cygwin網站。
開啟終端,也在bda/part3/vw資料夾中,並執行以下命令:
vw train_titanic.vw -f model.vw --binary --passes 20 -c -q ff --sgd --l1 0.00000001 --l2 0.0000001 --learning_rate 0.5 --loss_function logistic
讓我們分解一下vw呼叫的每個引數的含義。
-f model.vw − 表示我們將模型儲存在model.vw檔案中,以便以後進行預測
--binary − 將損失報告為具有-1,1標籤的二元分類
--passes 20 − 資料被使用20次來學習權重
-c − 建立快取檔案
-q ff − 在f名稱空間中使用二次特徵
--sgd − 使用常規/經典/簡單的隨機梯度下降更新,即非自適應、非歸一化和非不變。
--l1 --l2 − L1和L2範數正則化
--learning_rate 0.5 − 更新規則公式中定義的學習率α
下面的程式碼顯示了在命令列中執行迴歸模型的結果。在結果中,我們得到了平均對數損失和演算法效能的小型報告。
-loss_function logistic creating quadratic features for pairs: ff using l1 regularization = 1e-08 using l2 regularization = 1e-07 final_regressor = model.vw Num weight bits = 18 learning rate = 0.5 initial_t = 1 power_t = 0.5 decay_learning_rate = 1 using cache_file = train_titanic.vw.cache ignoring text input in favor of cache input num sources = 1 average since example example current current current loss last counter weight label predict features 0.000000 0.000000 1 1.0 -1.0000 -1.0000 57 0.500000 1.000000 2 2.0 1.0000 -1.0000 57 0.250000 0.000000 4 4.0 1.0000 1.0000 57 0.375000 0.500000 8 8.0 -1.0000 -1.0000 73 0.625000 0.875000 16 16.0 -1.0000 1.0000 73 0.468750 0.312500 32 32.0 -1.0000 -1.0000 57 0.468750 0.468750 64 64.0 -1.0000 1.0000 43 0.375000 0.281250 128 128.0 1.0000 -1.0000 43 0.351562 0.328125 256 256.0 1.0000 -1.0000 43 0.359375 0.367188 512 512.0 -1.0000 1.0000 57 0.274336 0.274336 1024 1024.0 -1.0000 -1.0000 57 h 0.281938 0.289474 2048 2048.0 -1.0000 -1.0000 43 h 0.246696 0.211454 4096 4096.0 -1.0000 -1.0000 43 h 0.218922 0.191209 8192 8192.0 1.0000 1.0000 43 h finished run number of examples per pass = 802 passes used = 11 weighted example sum = 8822 weighted label sum = -2288 average loss = 0.179775 h best constant = -0.530826 best constant’s loss = 0.659128 total feature number = 427878
現在我們可以使用我們訓練的model.vw來使用新資料生成預測。
vw -d test_titanic.vw -t -i model.vw -p predictions.txt
前面命令生成的預測並未歸一化到[0, 1]範圍。為此,我們使用sigmoid變換。
# Read the predictions
preds = fread('vw/predictions.txt')
# Define the sigmoid function
sigmoid = function(x) {
1 / (1 + exp(-x))
}
probs = sigmoid(preds[[1]])
# Generate class labels
preds = ifelse(probs > 0.5, 1, 0)
head(preds)
# [1] 0 1 0 0 1 0