資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究一位身高 1.5 米的觀察者距離一座 22 米高的塔 20.5 米。確定觀察者眼睛到塔頂的仰角。
已知
一位身高 \( 1.5 \) 米的觀察者距離一座 22 米高的塔 \( 20.5 \) 米。
要求
我們需要確定從他的眼睛到塔頂的仰角。
解答
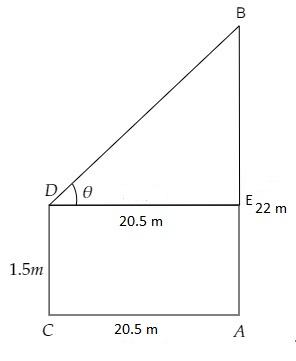
設 $AB$ 為塔，$CD$ 為觀察者，觀察者距離塔 \( 20.5\ m \)。
從圖中，
$AB = 22\ m, CD=1.5\ m, AC=20.5\ m$
這意味著，
$AE=CD=1.5\ m, DE=AC=20.5\ m$ 以及 $BE=22-1.5=20.5\ m$
設 \( \theta \) 為從觀察者眼睛到塔頂的仰角。
在 $\Delta \mathrm{BDE}$ 中，
$\tan \theta=\frac{\text { 垂直邊 }}{\text { 水平邊 }}$
$\Rightarrow \tan \theta=\frac{\mathrm{BE}}{\mathrm{DE}}$
$=\frac{20.5}{20.5}$
$=1$
$=\tan 45^{\circ}$ [因為 $\tan 45^{\circ}=1$]
$\Rightarrow \theta=45^{\circ}$
因此，從他的眼睛到塔頂的仰角為 $45^{\circ}$。
更新於: 2022 年 10 月 10 日
169 次瀏覽
廣告