有兩座寺廟，分別位於一條河的兩岸，正好相對。一座寺廟高 50 米。從這座寺廟的頂部，觀察到另一座寺廟的頂部和底部 的俯角分別為 30° 和 60°。求河流的寬度和另一座寺廟的高度。

已知

有兩座寺廟，分別位於一條河的兩岸，正好相對。一座寺廟高 50 米。

從這座寺廟的頂部，觀察到另一座寺廟的頂部和底部的俯角分別為 30° 和 60°。

要求

我們需要求出河流的寬度和另一座寺廟的高度。

解答

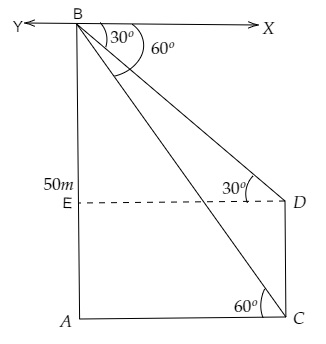
設 AB 為第一座寺廟，CD 為第二座寺廟，AC 為河流的寬度。

從 B 點觀察第二座寺廟底部的俯角為 60°，從 B 點觀察第二座寺廟頂部的俯角為 30°。

設第二座寺廟的高度為 h 米。

從圖中可以看出，

∠BDE = 30°，AB = 50 米，∠BCA = 60°

這意味著，

AE = CD = h 米，BE = 50 - h 米

AC = ED = x 米

在△BCA 中，

tan 60° = BA/AC = 50/x

√3 = 50/x

x = 50/√3.........(i)

在△BDE 中，

tan 30° = BE/DE = (50 - h)/x

1/√3 = (50 - h)/(50/√3)               [根據 (i)]

(50/√3) × (1/√3) = 50 - h 米

50/3 = 50 - h 米

h = 50 - 50/3 = (50(3) - 50)/3

h = 100/3

h = 33.33 米

x = 50/1.732 = 28.83 米

因此，河流的寬度為 28.83 米，另一座寺廟的高度為 33.33 米。  

Tutorialspoint

更新於: 2022 年 10 月 10 日

150 次瀏覽

開啟你的 職業生涯

完成課程獲得認證

開始學習